問題
配電線に100〔kW〕、遅れ力率60〔%〕の三相負荷が接続されている。
この受電端に45〔kvar〕の電力用コンデンサを接続した。
次の(a)及び(b)に答えよ。
ただし、電力用コンデンサ接続前後の電圧は変わらないものとする。
(a) 電力用コンデンサを接続した後の受電端の無効電力〔kvar〕の値として、最も近いのはどれか?
(1) 56
(2) 60
(3) 75
(4) 88
(5) 133
(b) 電力用コンデンサ接続前と後の力率〔%〕の差の大きさとして、最も近いのはどれか?
(1) 5
(2) 15
(3) 25
(4) 55
(5) 75
基礎知識(解き方)
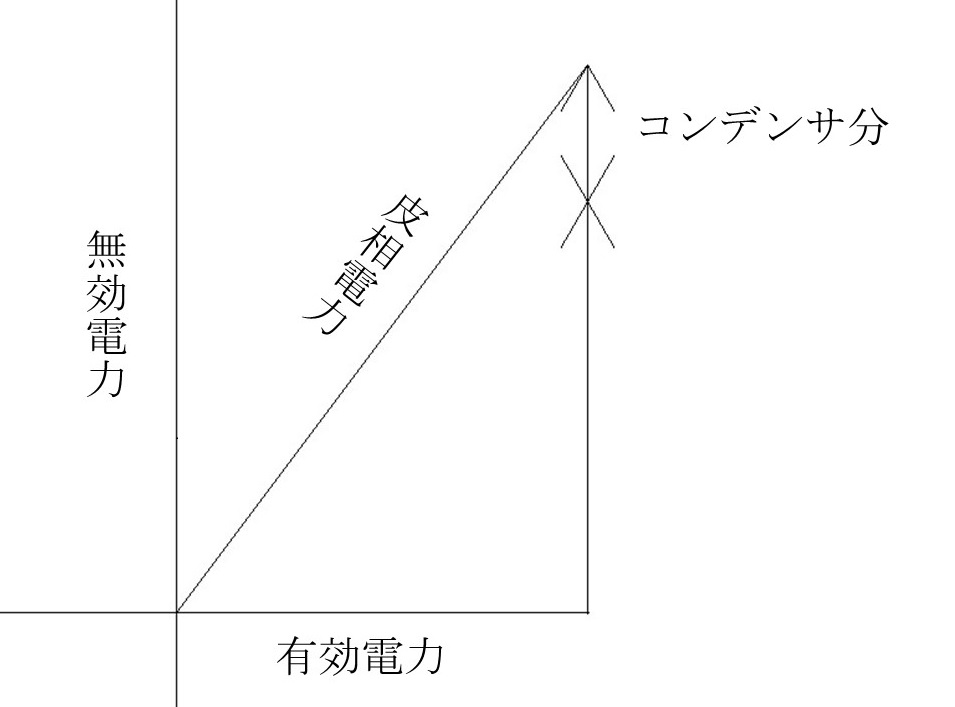
今回の問題をベクトル図に表すと下図のようになります。
(遅れ力率をプラスに取っています。)
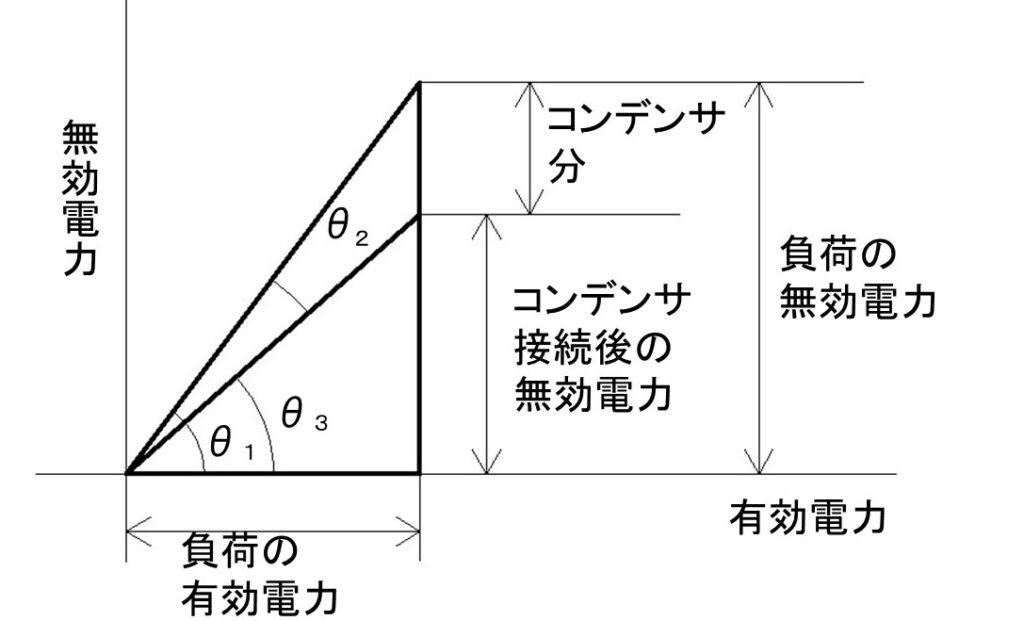
(a)の解き方としては
問題文に100〔kW〕とあります。
〔W〕で表示されているので、これは有効電力のことです。
有効電力「$P$」〔W〕は、皮相電力「$S$」〔VA〕に力率「 $cos\ \theta$ 」を掛けたものです。
式で書くと、$P\ =\ S\ \times\ cos\ \theta$ ですよね。
では、無効電力「$Q$」〔var〕は、皮相電力「$S$」〔VA〕に「 $sin\ \theta$ 」を掛けたものです。
「 $sin\ \theta$ 」 を求めるには、「 $sin^2\ \theta\ \times\ cos^2\ \theta\ =\ 1$ 」 の公式から
「 $sin\ \theta\ =\ \sqrt{\ 1\ -\ cos^2\ \theta\ }$ 」 で求めます。
そして、電力用コンデンサは進み無効電力を供給するので、遅れ無効電力を打ち消す働きをします。
(b)解き方としては
力率( $cos\ \theta$ )は、コサインなので、$cos\ \theta\ =\ \cfrac{{有効電力}}{{皮相電力}}$ です。
皮相電力は、三平方の定理(${斜辺}\ ^2={横辺}\ ^2+{縦辺}\ ^2$)より
${皮相電力}\ =\ \sqrt{{有効電力}\ ^2\ +\ {無効電力}\ ^2\ }$ で求めます。
解答
(a)の正解は(4)
(b)の正解は(2)
(a)まずは、電力用コンデンサが接続される前の皮相電力$S_b$〔kVA〕を求めます。
$P\ =\ S\ \times\ cos\ \theta$ より、$S\ =\ \cfrac{P}{\ cos\ \theta\ }$ となり、
$S_b=\cfrac{100}{0.6}\fallingdotseq166.66$ 〔VA〕
電力用コンデンサ接続前の無効電力 $Q_b$ 〔kvar〕は、皮相電力 $S_b$ 〔kVA〕に $sin\theta$ を掛けたものですが、
$sin\theta$ は、 $sin\ \theta\ =\ \sqrt{\ 1\ -\ cos^2\ \theta\ }$ なので、
$Q_b=166.66\times\sqrt{1-0.6^2} \fallingdotseq 133.33$ 〔kvar〕
電力用コンデンサを接続することにより、三相負荷の遅れ無効電力と電力用コンデンサの進み無効電力が相殺されます。
よって、電力用コンデンサを接続した後の受電端の無効電力 $Q_a$ 〔kvar〕は、
$Q_a=133.33-45=88.33$ 〔kvar〕 となります。
最も近いのは、(4)の88です。
(b)電力用コンデンサを接続する前の力率は遅れ力率 $cos\ \theta_1\ =$ 60〔%〕と問題文に書いてあります。
では、電力用コンデンサを接続した後の力率は、$cos\ \theta_2\ =\ \cfrac{{有効電力}}{{接続後の皮相電力}}$ です
また、 ${皮相電力}\ =\ \sqrt{{有効電力}\ ^2\ +\ {無効電力}\ ^2\ }$ ですから、
$cos\theta_2=\cfrac{100}{\sqrt{100^2+88.33^2\ }}\fallingdotseq74.95$ になります。
電力用コンデンサを接続した前と後の力率の差は、
$cos\theta_3=cos\theta_1-cos\theta_2=74.95-60=14.95\fallingdotseq15$ となり、
最も近いのは、(2)の15です。
まとめ
この問題はサービス問題です。確実に取りましょう。
もう、分かっているはずのことを少し書きます。
まず、問題文に単位〔W〕と出てくると、有効電力のことです。
同様に、単位〔VA〕と出てくると、皮相電力のことです。
有効電力と書かれていないからと悩まないようにしましょう。
$sin^2\theta+cos^2\theta=1^2=1$ も三平方の定理ですよね。
次に、電力用コンデンサを接続しても、有効電力は変わりません。
電力用コンデンサは、進み無効電力のみを供給します。
ちなみに、問題文に「 電力用コンデンサ接続前後の電圧は変わらないものとする 」とありますよね。
これって、負荷の有効電力が同じでも、無効電力が変わると皮相電力も変わります。
皮相電力が変わると、電流が変わります。
電流が変わると、電圧降下の量が変わります。
すると、受電端電圧が変わってくることになり、皮相電力も変わってくることになります。
他の問題で、受電端電圧を調整する装置として、電力用コンデンサや分路リアクトルがあると書かれているのを見たことがある人もいると思います。
この問題では、受電端電圧が変わってくると問題が解けないので、その注意書きです。

コメント