問題
電圧33〔KV〕、周波数60[Hz]、こう長2[Km]の交流三相3線式地中電線路がある。
ケーブルの心線1線当たりの静電容量が0.24[マイクロF/km]、誘電正接が0.03[%]であるとき、このケーブルの心線3線合計の誘電体損[W]の値として最も近いのはどれか?
(1)9.4
(2)19.7
(3)29.5
(4)59.1
(5)177
基礎知識
送電ケーブルには、電価を溜める静電容量と電線の抵抗を持っています。
今回の問題では、静電容量は考えていますが、抵抗については考えていません。
問題文に書かれていないので。
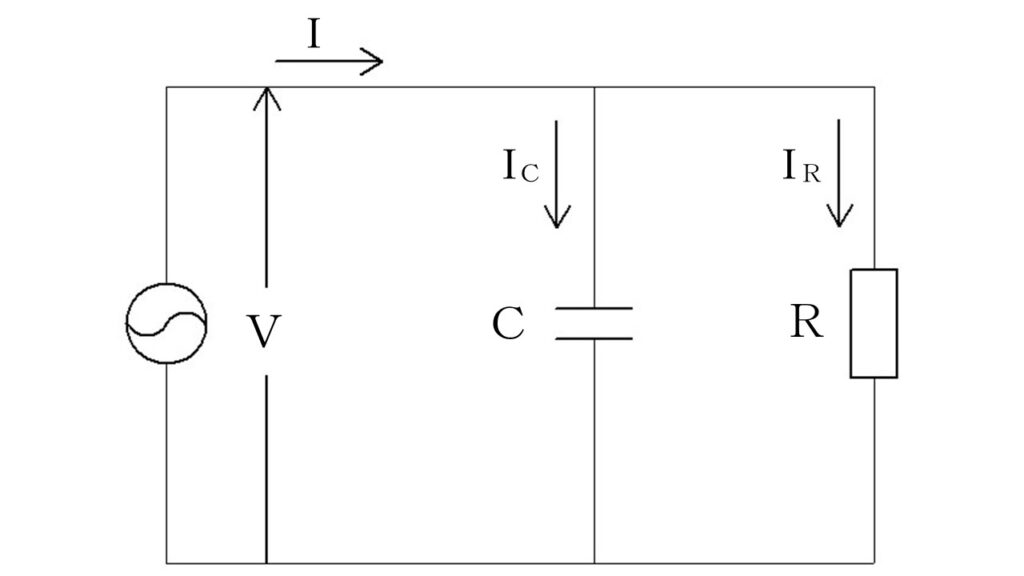
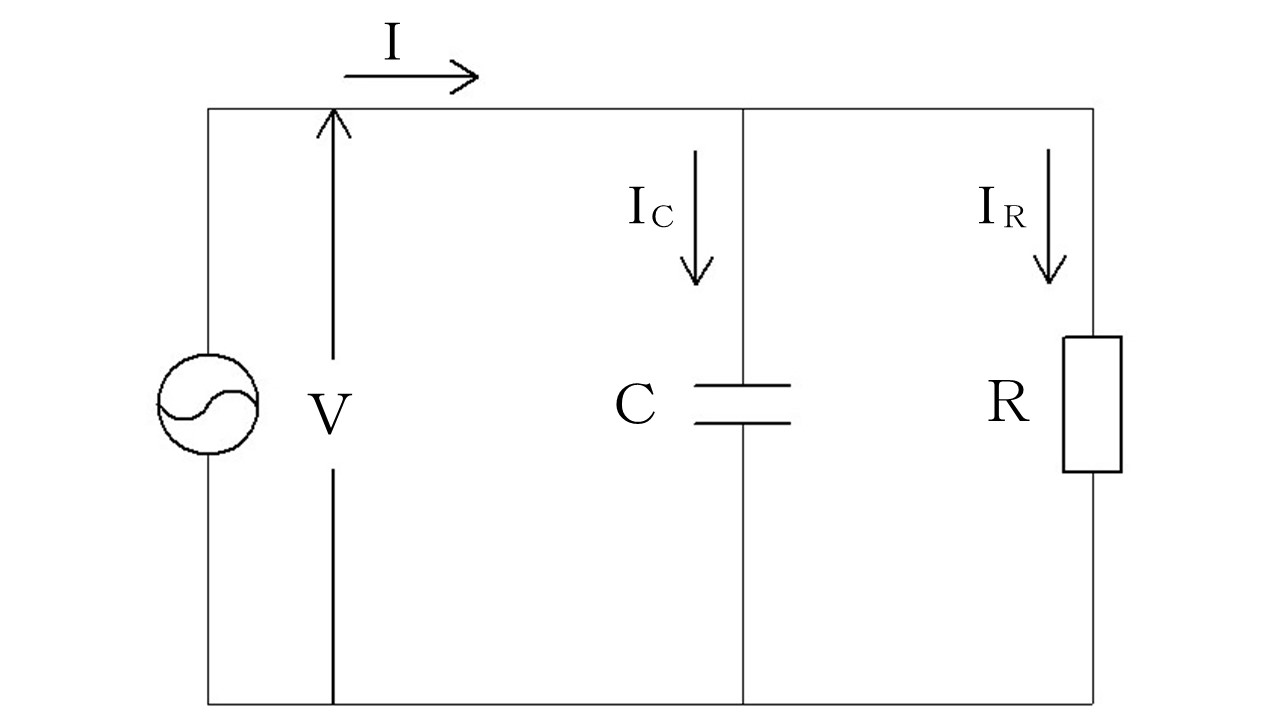
上の図は、送電線一線当たりの等価回路です。
ここにコンデンサ(静電容量「C」)と抵抗「R」があります。
この抵抗「R」は電線の持つ抵抗ではありません。
コンデンサに交流電源を加えると、電荷の移動が発生します。
(上に⊕の電荷が溜まる半周期と⊖の電荷が溜まる半周期が交互に入れ替わるため)
この電荷の移動に、電圧より遅れが発生します。
この遅れ分の等価回路として、抵抗分が入ってきます。
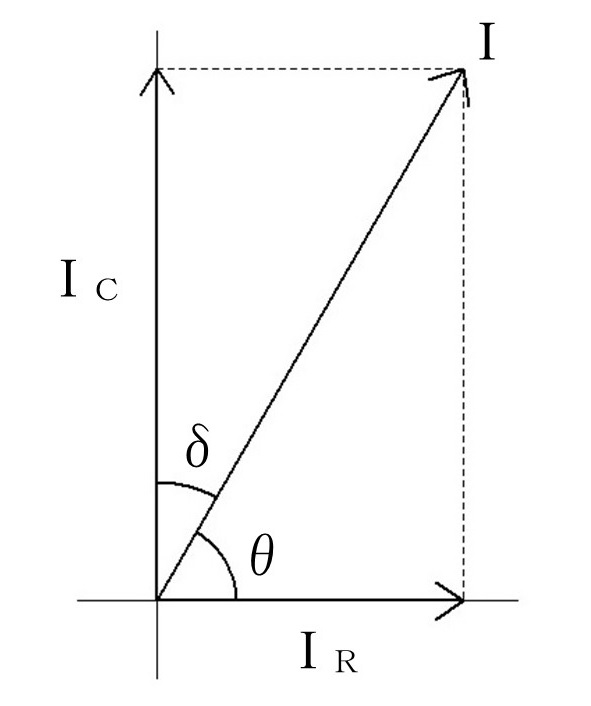
ベクトル図で表すと、上の図のようになります。
ここで、誘電正接角 $\delta$ を使った $tan\ \delta$ が誘電正接です。
では、誘電体損を $W_d$ とすると、$W_d\ =\ V\ \times\ I_R$ です。
(単位が「W」なので、上のベクトル図の有効電力 $W_d\ =\ V\ \times\ I\ cos\ \theta$ より、
上の式が出てきます。)
誘電正接は、上の図を寝かせると静電正接は $tan\ \delta\ =\ \cfrac{I_R}{I_C}$ と表せます。
これを $I_R$ について解くと、$I_R\ =\ I_C\ tan\ \delta$ と表せます。
また、オームの法則より $I_C\ =\ \cfrac{V}{Z}\ =\ \omega\ C\ V$ と表すことができ、
これを代入すると
$I_R\ =\ \omega\ C\ V\ tan\ \delta$ となります。
これを誘電体損の式に代入すると、$W_d\ =\ \omega\ C\ V^2\ tan\ \delta$ となります。
ここで、$\omega\ =\ 2\ \pi\ f$ を代入すると、
$W_d\ =\ 2\ \pi\ f\ C\ V^2\ tan\ \delta$ となります。
これが、誘電体損の公式です。
解答
正解は、(4)です。
この問題は、基礎知識に書いた誘電体損の公式を覚えているかどうかの問題です。
周波数 $f$ は60〔Hz〕、電圧 $V$ は33〔KV〕、静電容量 $C$ は0.24〔μF/km〕の2〔km〕分で、0.48〔μF〕、誘電正接 $tan\ \delta$ は0.03%なので、
$W_d\ =\ 2\ \pi\ f\ C\ V^2\ tan\ \delta$
$=\ 2\ \times\ 3.1416\ \times\ 60\ \times\ 0.48\ \times\ 10^{-6}\times\ (33\ \times\ 10^3)^2\ \times\ 0.03\ \times\ 10^{-2}$
$\fallingdotseq\ 59.1184$
となります。
まとめ
この問題は、誘電体損の公式を覚えていれば、直ぐに解けます。
しかし、毎回出る公式ではないので、覚えている人も少ないと思います。
そこで、ベクトル図と導出方法を覚えておいて、試験場で導き出すのはどうでしょうか?
短い時間の中では無理だと思う人は、この問題は捨てましょう。
重箱の隅の問題は捨てるのも、電験合格の一つのテクニックです。
また、計算の時の単位(μ、k、%)等は、「10」の指数で表示しておきましょう。
この問題の場合は、「μ」なら $10^{-6}$ 、「k」なら $10^3$ 、「%」なら $10^{-2}$ といった感じです。
計算間違いが、少し減ります。
コメント