問題
こう長 2〔km〕の交流三相3線式の高圧配電線路があり、その端末に受電電圧 6500〔V〕、遅れ力率 80〔%〕で消費電力 400〔KW〕の三相負荷が接続されている。
いま、この三相負荷を力率 100〔%〕で消費電力 400〔kW〕のものに切り替えたうえで、受電電圧を 6500〔V〕に保つ。
高圧配電線路での電圧降下は、三相負荷を切り替える前と比べ何倍になるか?
ただし、高圧配電線路の 1線当たりの線路定数は、抵抗が 0.3〔Ω/km〕、誘導性リアクタンスが 0.4〔Ω/km〕とする。
また、送電端電圧と受電端電圧との相差角は小さいものとする。
(1)1.6
(2)1.3
(3)0.8
(4)0.6
(5)0.5
基礎知識
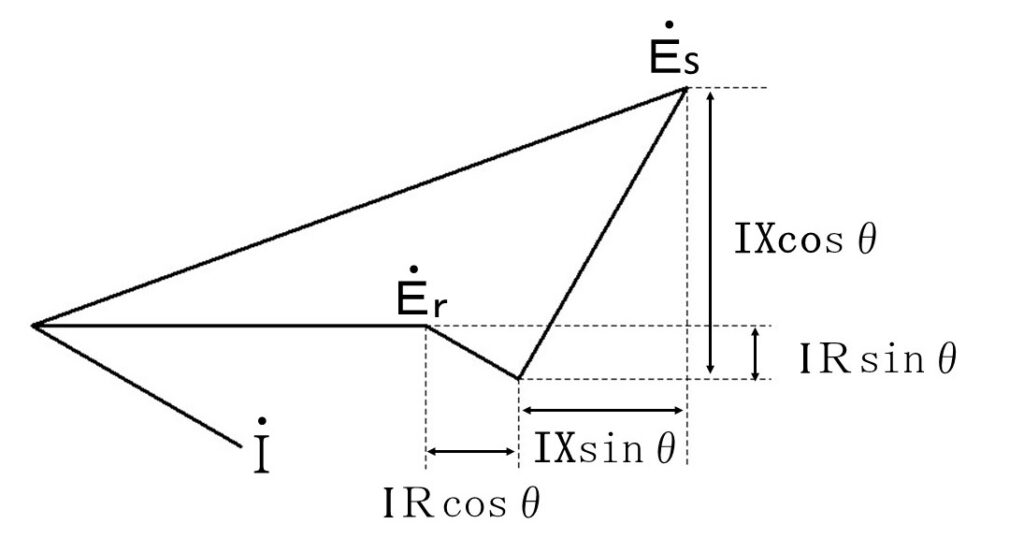
基礎と言えるかは別にして、前提知識として、電圧降下の近似式があります。
$e=\sqrt{3}\ I\ (\ R\ cos\theta\ +\ X\ sin\theta\ )$ というものです。
ここで、$e$ は電圧降下分、$I$ は線電流、$R$ は電線路抵抗、$X$ は電線路リアクタンス、$cos\theta$ は負荷力率です。
今回は、この「電圧降下の近似式って何?」を説明しようかと思います。
図の送電端相電圧が $\dot{E_s}$(ベクトル)、受電端相電圧が $\dot{E_r}$(ベクトル)です。
線電流が $\dot{I}$(ベクトル)で、線路インピーダンスが $\dot{Z}$(ベクトル)です。
(ベクトルのドットが見づらいので、後ろに(ベクトル)と書きました。)
送電端電圧=受電端電圧+電圧降下 となりますよね。
式で書くと、$\dot{E_s}\ =\ \dot{E_r}\ +\ \dot{Z}\ \dot{I}$ となります。
ここで、$\dot{Z}\ =\ (\ R\ +\ j\ X)$ です。
また、$\dot{I}\ =\ I\ (cos\theta\ -\ j\ sin\theta)$ と表すことができます。
これを上の式に代入すると、( ${E_r}$ を基準とします。)
$\dot{E_s}\ =\ E_r\ +\ (R\ +\ j\ X)\ \times\ I\ (cos\theta\ -\ j\ sin\theta)$
右辺を展開すると、
$E_r\ +\ (R\ I\ cos\theta\ +\ X\ I\ sin\theta)\ +\ j\ (-R\ I\ sin\theta\ +\ X\ I\ cos\theta)$
電圧降下の部分は、
$(R\ I\ cos\theta\ +\ X\ I\ sin\theta)\ +\ j\ (-R\ I\ sin\theta\ +\ X\ I\ cos\theta)$
このうち $j\ (-R\ I\ sin\theta\ +\ X\ I\ cos\theta)$ の部分(縦軸の部分)が小さいので無視することができる。
今回の問題文には、「送電端電圧と受電端電圧との相差角は小さいものとする」と書かれているので、無視しなさいということです。
相電圧における電圧降下分は、$R\ I\ cos\theta\ +\ X\ I\ sin\theta$ です。
線間電圧の電圧降下分は、$e=\sqrt{3}\ (R\ I\ cos\theta\ +\ X\ I\ sin\theta)$ です。
$I$ を括り出して、$e=\sqrt{3}\ I\ (\ R\ cos\theta\ +\ X\ sin\theta\ )$ です。
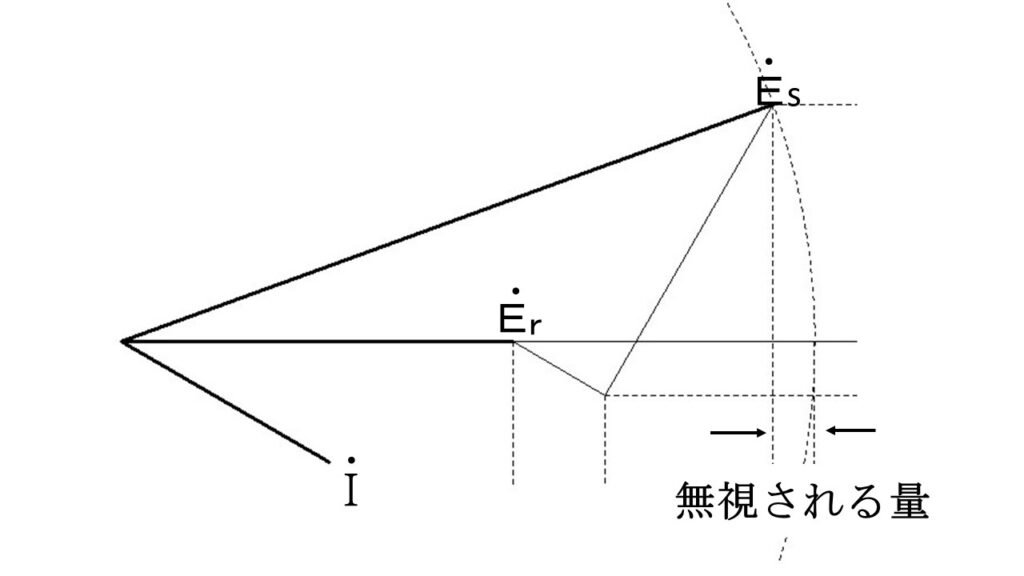
ベクトル図で見ているので、縦軸分を無視して良いものか?と思いますが、単純に数字だけ(スカラー)で見ると微々たるものです。
解答
正解は、(5)です。
まずは、1線当たりの線路定数のうち、抵抗分が 0.3〔Ω/km〕の2〔km〕分なので、
$R\ =\ 0.3\ \times\ 2\ =\ 0.6$
誘導性リアクタンス分が0.4〔Ω/km〕の2〔km〕分なので、
$X\ =\ 0.4\ \times\ 2\ =\ 0.8$
切り替え前の線電流は、電力の式 $P\ =\ \sqrt{3}\ V\ I\ cos\theta$ より
$I_1\ =\ \cfrac{P}{\sqrt{3}\ V\ cos\theta}$〔A〕となります。
数値を代入すると、$I_1\ =\ \cfrac{400,000}{\sqrt{3}\ \times\ 6,500\ \times\ 0.8}\ \fallingdotseq\ 44.41$ 〔A〕となります。
切り替え前の電圧降下は、近似式より、
$e_1\ =\ \sqrt{3}\ I_1\ (R\ cos\theta\ +\ X\ sin\theta)$ より、
$e_1\ =\ \sqrt{3}\ \times\ 44.41\ \times\ (0.6\ \times\ 0.8\ +\ 0.8\ \times\ \sqrt{1\ -\ 0.8^2})\ \fallingdotseq\ 73.84$
同様に、切り替え後の線電流は、
$I_2\ =\ \cfrac{400,000}{\sqrt{3}\ \times\ 6,500\ \times\ 1}\ \fallingdotseq\ 35.53$ 〔A〕となります。
切り替え後の電圧降下は、
$e_2\ =\ \sqrt{3}\ \times\ 35.53\ \times\ (0.6\ \times\ 1\ +\ 0.8\ \times\ 0)\ \fallingdotseq\ 36.92$
切り替え後の電圧降下を、切り替え前の電圧降下と比べると、
$\cfrac{e_2}{e_1}\ =\ \cfrac{36.92}{73.84}\ =\ 0.5$ 〔倍〕になります。
まとめ
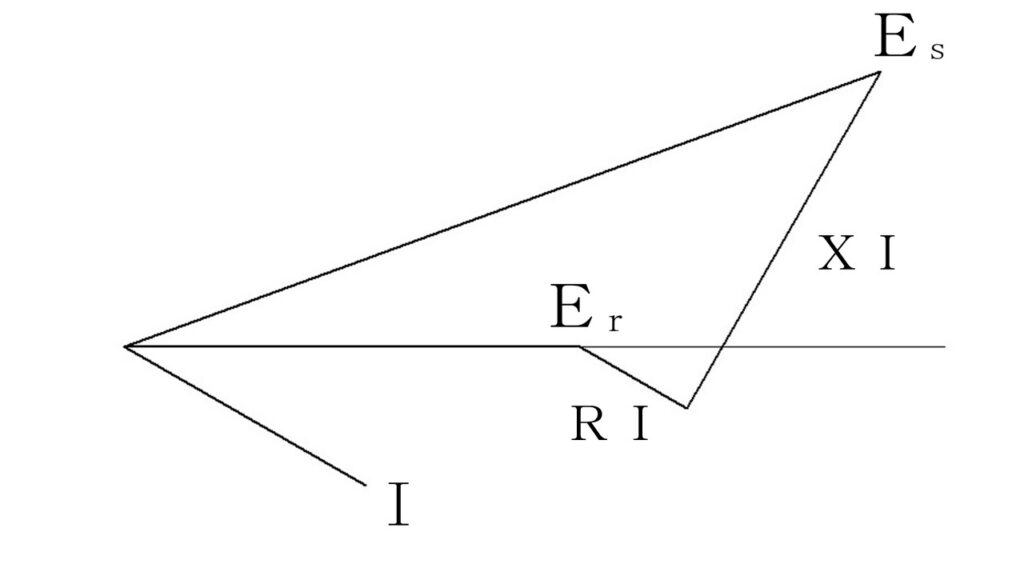
この図は、受電端電圧・送電端電圧の基本図形です。
これからもたびたび出てきますので、よろしくお願いします。
コメント