問題
水力発電所において、有効落差100〔m〕、水車効率92〔%〕、発電機効率94〔%〕、定格出力2500〔kW〕の水車発電機が80〔%〕負荷で運転している。
このときの流量〔m³/s〕の値として、最も近いのはどれか?
(1) 1.76
(2) 2.36
(3) 3.69
(4) 17.3
(5) 23.1
必要な公式
$P=gHQ\eta$
$P$ :出力〔kW〕
$g$ :重力加速度=9.8〔$m/s^2$〕
$H$:有効落差〔$m$〕
$Q$:流量〔$m^3$〕
$\eta$:効率
解答
正解は(2)
公式 $P=gHQ\eta$ より、
$Q$ について解くと、$Q=\cfrac{P}{gH\eta}$ と書けます。
ここで、効率 $\eta$ は水車効率と発電機効率を掛け合わせものですので、
$\eta=0.92\times 0.94\times 100=86.48$ 〔%〕となります。
また題意より、80%負荷で運転しているので、出力 $P=2500\times0.8=2000$ となります。
その他、数値を代入すると、$Q=\cfrac{2000}{9.8\times100\times0.8648}\fallingdotseq2.36$
解説
この問題は、単純に公式 $P=gHQ\eta$ を覚えているかにかかっています。
重力加速度を $9.8$ と置かずに $g$ としたのは、第二次世界大戦後のGHQ(連合国軍最高司令官総司令部)を想起してもらうためです。(マッカーサー元帥を知らない人には、ごめんなさい。)
「水力発電の出力 $P$ は、連合国軍最高司令官総司令部 $gHQ$ の効率 $\eta$ にかかっている。」(なんのこっちゃ)
この式は、確実に覚えておきましょう。
たま~に出てくる問題ですが、ひねる箇所がないのか、素直な問題が多いですよ。
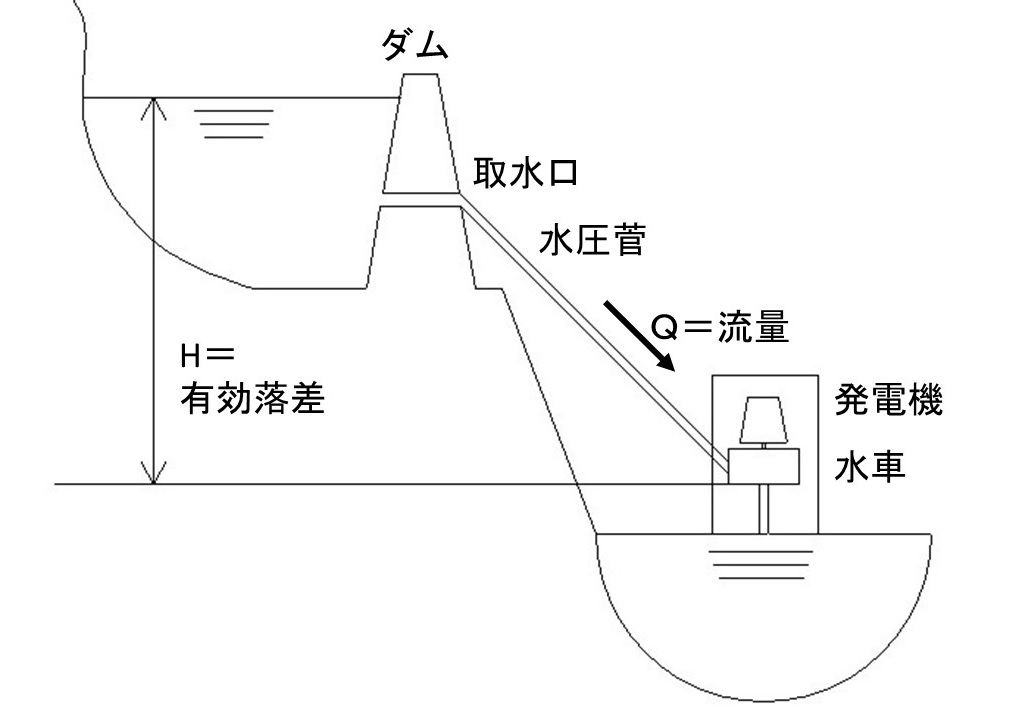
次に、上の図の有効落差「H」についてですが、見る資料により取り方が違っているかもしれません。
それは、水車の出口からその下の水面までの水の流れの処理の仕方により変わってきます。
今回は、水車下端までにしています。
吸出し管で水車下端から放水面までの圧力を有効利用している場合の有効落差は、ダム水面から放水面までになります。
また、今回は「総落差=有効落差」としていますが、
損失落差を考える場合は、「総落差=有効落差+損失落差」になります。
細かいことなので気にすることはないと思いますが、後学のために一言添えました。
まとめ
今回、重力加速度 $g=9.8\ [m/s^2]$ を常識の範囲内として話を進めてきました。
もし覚えていないのならば、覚えておきましょう。
この問題は、覚えておくことも少なく、ひねりもなく、なので、サービス問題です。
確実に取れるようにしておいてください。
コメント