問題
図のような交流三相3線式の系統がある。各系統の基準容量と基準容量をベースにした百分率インピーダンスが図に示された値であるとき、次の(a)及び(b)に答えよ。
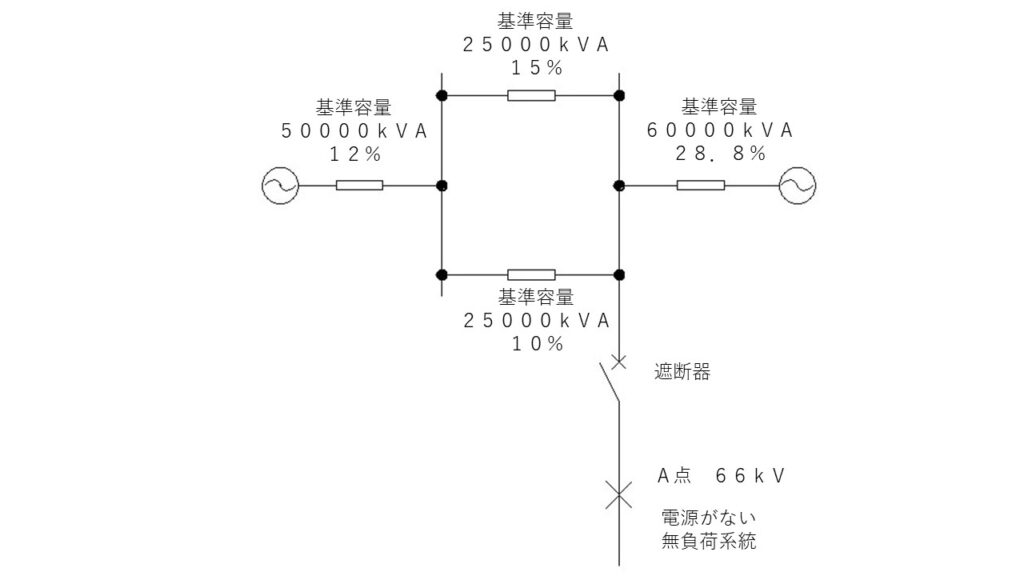
(a)系統全体の基準容量を50000〔kVA〕に統一した場合、遮断器の設置場所からみた合成百分率インピーダンス〔%〕の値として、正しいのはどれか?
(1)4.8
(2)12
(3)22
(4)30
(5)48
(b)遮断器の投入後、A点で三相短絡事故が発生した。
三相短絡電流〔A〕の値として、最も近いのはどれか?
ただし、線間電圧は66〔kV〕とし、遮断器からA点までのインピーダンスは無視するものとする。
(1)842
(2)911
(3)1458
(4)2104
(5)3645
基礎知識
百分率インピーダンス、またの名をパーセントインピーダンスと言い、「%$Z$」と表します。
発電機、送配電線路、変圧器等に用いられます。
意味合いは、「定格電流が流れた時の電圧降下の定格相電圧に対する比をパーセント表示したもの」のことです。
ここで、入力端子から出力端子までのインピーダンスを $Z$〔Ω〕 、定格電流を $I_n$〔A〕 、定格相電圧を $E_n$ 〔V〕、とすると、
電圧降下は、$Z\ I_n$ なので、%$Z=\cfrac{Z\ I_n}{E_n}\times100$
になります。
定格線間電圧 $V_n$ に対しては、%$Z=\cfrac{X\ I_n}{\cfrac{V_n}{\sqrt3}}\times100$
となります。
こ百分率インピーダンスは、定格(基準)容量に比例します。
例えば、A系統の基準容量を $S_a$ 〔kVA〕、そのときの百分率インピーダンスを「 $a$ 」とします。
これを統一基準容量 $S_n$ 〔kVA〕に換算する場合、そのときの百分率インピーダンスを「 $x$ 」とすると、
次の比が成り立ちます。
$S_a\ :\ S_n\ =\ a\ :\ x$
比の計算において、「外側の積}」=「内側の積」なので、
$S_a\ \times\ x\ =\ S_n\ \times\ a$
$x\ =\ \cfrac{S_n}{S_a}\ \times\ a$
日本語で表すと、${統一基準容量での%Z}=\cfrac{統一基準容量}{系統基準容量}\times{系統基準容量での%Z}$ となります。
(b)では、三相短絡電流を求める問題となっています。
これも、百分率インピーダンスを式変形して、短絡電流を求めることができます。
まず、短絡電流を $I_s$ 、定格電流を $I_n$ とします。
ここで、短絡点の相電圧は「0〔V〕」なので、電圧降下で考えると、
$I_s\ \times\ Z\ =\ E_n$
これから $I_s$ を求めると、$I_s\ =\ \cfrac{E_n}{Z}$ と表せます。
これを、%$Z$ の式に代入します。
%$Z\ =\ \cfrac{Z}{E_n}\ \times\ I_n\ \times\ 100$
$=\ \cfrac{1}{I_s}\ \times\ I_n\ \times100$
$=\ \cfrac{I_n}{I_s}\ \times\ 100$ と表せます。
これを、短絡電流 $I_s$ について解くと、
$I_s\ =\ I_n\ \times\ \cfrac{100}{{%}Z}$
ちなみに、定格電流 $I_n$ は、基準容量を $S_n$ 、定格線間電圧を $V_n$ とすると、
$S_n\ =\ \sqrt3\ V_n\ \times\ I_n$ より、
$I_n\ =\ \cfrac{S_n}{\sqrt3\ V_n}$ で求められます。
解答
(a)の正解は、(5)です。
(a)この問題を解くときは、まずは問の図を書き換えます。
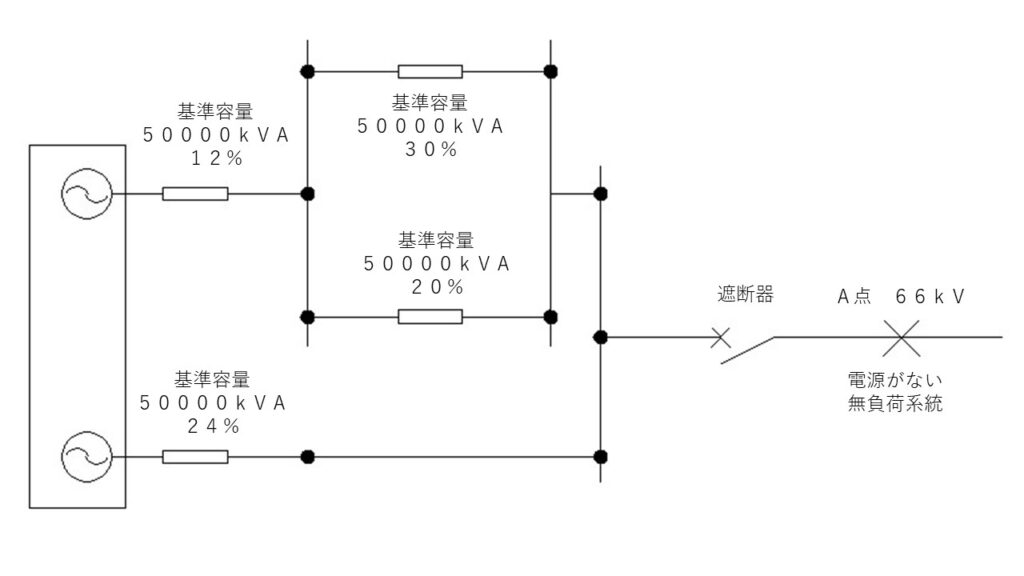
電源を左側に集めて、書き換えます。
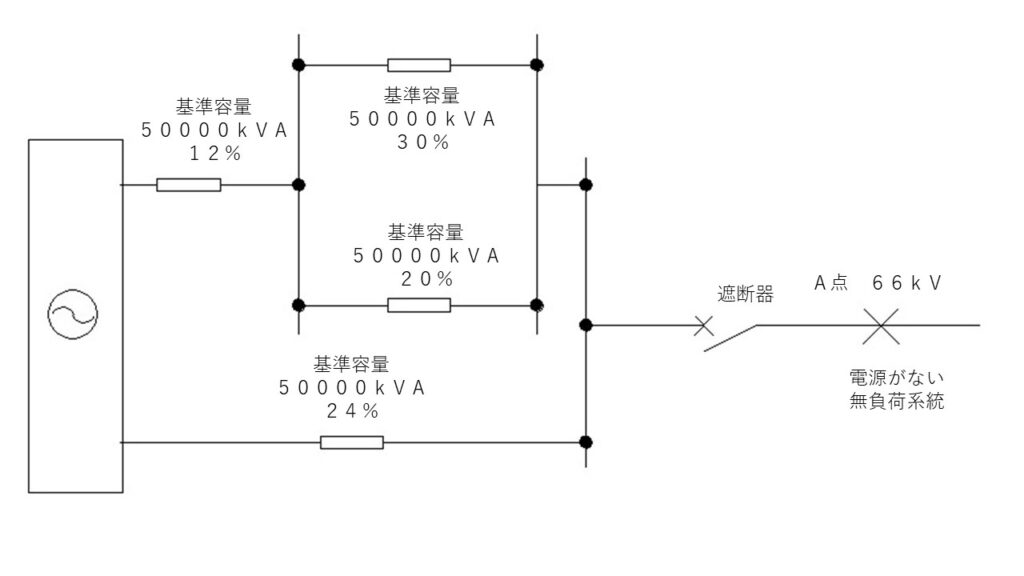
それから、電源を一つにまとめます。
この図を基に、合成百分率インピーダンスを求めます。
次に、全ての百分率インピーダンスを50000〔kVA〕基準容量の百分率インピーダンスに換算します。
基準容量25000〔kVA〕の15%の百分率インピーダンスを基準容量50000〔kVA〕に変換すると、
$\cfrac{50000}{25000}\times15=30$ で30%
基準容量25000〔kVA〕の10%の百分率インピーダンスを基準容量50000〔kVA〕に変換すると、
$\cfrac{50000}{25000}\times10=20$ で20%
基準容量60000〔kVA〕の28.8%の百分率インピーダンスを基準容量50000〔kVA〕に変換すると、
$\cfrac{50000}{60000}\times28.8=24$ で24%になります。
次に、合成抵抗を求める要領で、合成百分率インピーダンスを求めます。
30%と20%の並列合成百分率インピーダンスを求めます。
$\cfrac{30+20}{30\times20}=12$ となり、12%です。
この12%に直列に12%が接続されているので、
$12+12=24$ となり、上の合成百分率インピーダンスは24%です。
次に、24%の並列合成百分率インピーダンスを求めます。
$\cfrac{24+24}{24\times24}=12$ となり、全体の合成百分率インピーダンスは12%です。
(b)の正解は、(5)です。
まずは、定格電流 $I_n$ 〔kA〕を求めます。
基準容量 $S_n\ =\ 50000$ 〔kVA〕、定格電圧 $V_n\ =\ 66$ 〔kV〕ですから、
$I_n\ =\ \cfrac{S_n}{ \sqrt3\ V_n}\ =\ \cfrac{50000}{\sqrt3\ \times\ 66}\ \fallingdotseq\ 437.39$
次に、短絡電流 $I_s$ を求めます。
$I_s\ =\ I_n\ \times\ \cfrac{100}{{%}Z}\ =\ 437.39\ \times\ \cfrac{100}{12}\ =\ 3644.92\ \fallingdotseq\ 3645$
となり、短絡電流は3645〔A〕です。
まとめ
百分率インピーダンスとは、定格電流が流れた時の電圧降下と定格電圧との比になります。
これは、電験2種の2次試験、電力・管理の問題には常識のごとく出てきますが、3種ではどうかと思います。
私個人的には、捨てて良い分野だと思います。
電験2種を受けるつもりの人で、時間がある人は勉強してください。
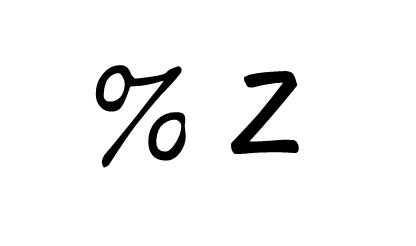
コメント