問題
交流三相3線式1回路の送電線路があり、受電端に遅れ力率角 $\theta$ 〔rad〕の負荷が接続されている。
送電端の線間電圧を $V_s$ 〔V〕、受電端の線間電圧を$V_r$ 〔V〕、その間の相差角は $\delta$ 〔rad〕である。
受電端の負荷に供給されている三相有効電力〔W〕を表す式として、正しいのはどれか?
ただし、送電端と受電端の間における電線1線当たりの誘導性リアクタンスは $X$ 〔Ω〕とし、線路の抵抗、静電容量は無視するものとする。
(1)$\cfrac{V_sV_r}{X}cos\ \delta$
(2)$\cfrac{\sqrt{3}V_sV_r}{X}cos\ \theta$
(3)$\cfrac{V_sV_r}{X}sin\ \delta$
(4)$\cfrac{\sqrt{3}V_sV_r}{X}sin\ \delta$
(5)$\cfrac{V_sV_r}{Xsin\ \delta}cos\ \theta$
基礎知識
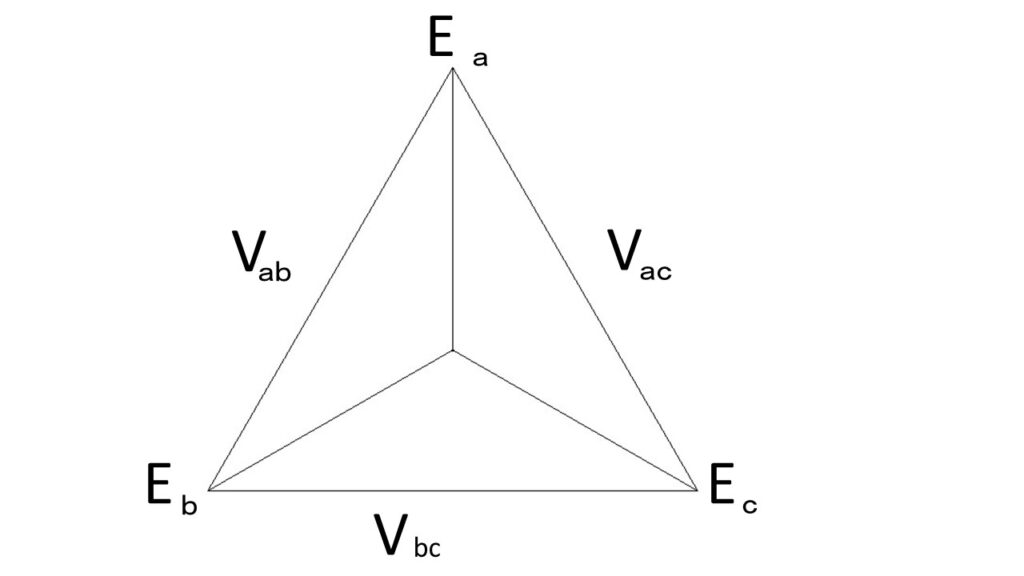
線間電圧を $V$ と表し、相電圧を $E$ と表す。
よって、$V=\sqrt{3}E$ となります。
これは、交流の問題を考えるときの常識ですので、間違えることなく覚えておいてください。
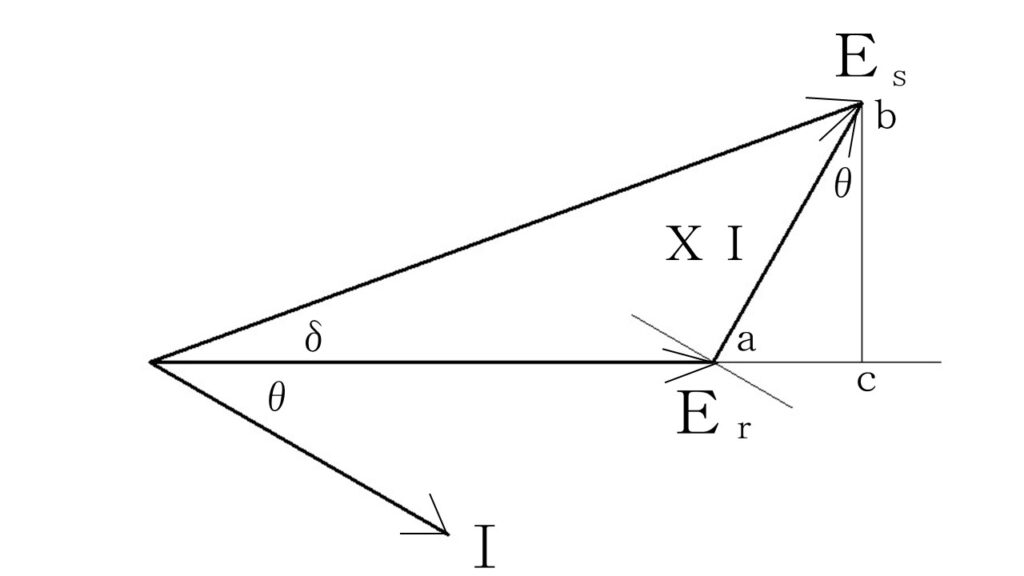
次に、送電端電圧と受電端電圧の関係です。
送電端電圧の相電圧を $\dot{E}_s$ として、受電端電圧の相電圧を $\dot{E}_r$ とします。
また、電流を $\dot{I}$ とし、送電端と受電端の1線当たりのリアクタンスを $X$ とします。
送電端電圧は、受電端電圧に電圧降下分を足したものとなります。
式で書くと、$\dot{E}_s=\dot{E}_r+X\dot{I}$ となります。
$\dot{I}$ と、点 $a$ を通る補助線とは、平行です。
この場合の電圧は、相電圧 $E$ で考えます。
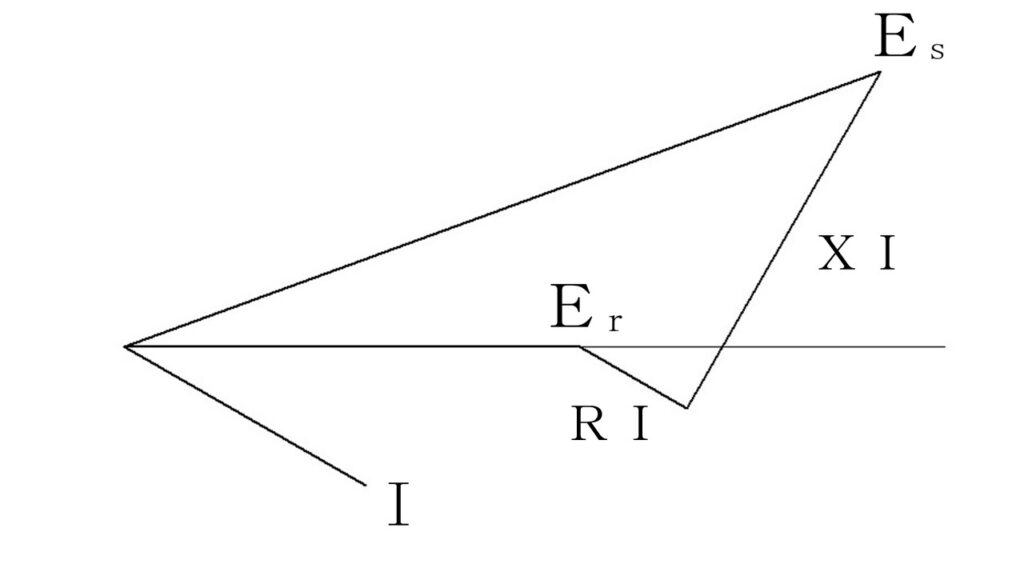
リアクタンス $X$ ではなく、インピーダンス $Z$ で考えるときは、上の図になります。
$\dot{I}$ と、$RI$ は、平行です。
また、有効電力 $P$ についてですが、線間電圧 $V$ を使います。
有効電力の式 $P=\sqrt{3}\ V\ I\ cos\theta$ の電圧は、線間電圧 $V$ です。
解答
正解は(3)です。
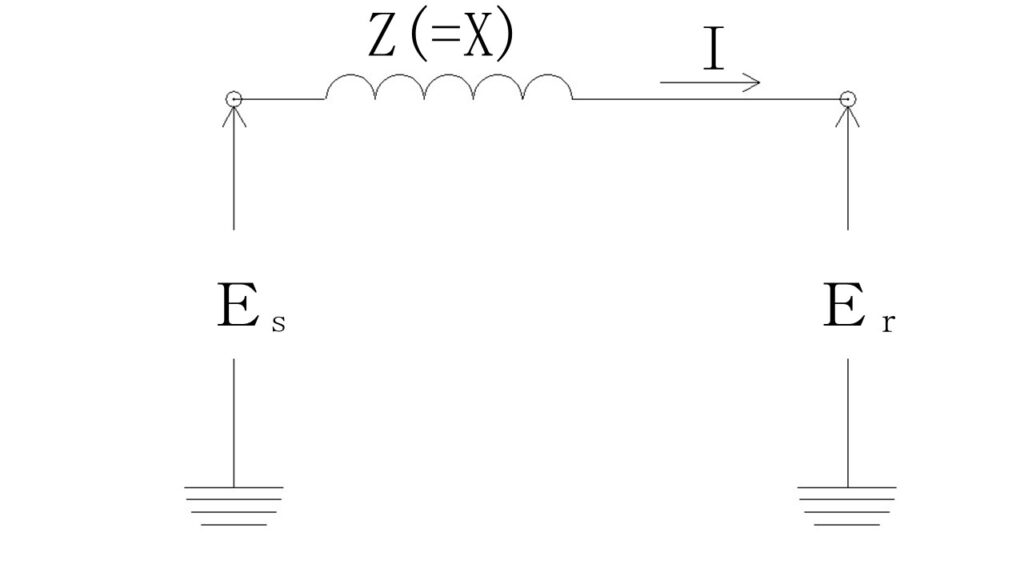
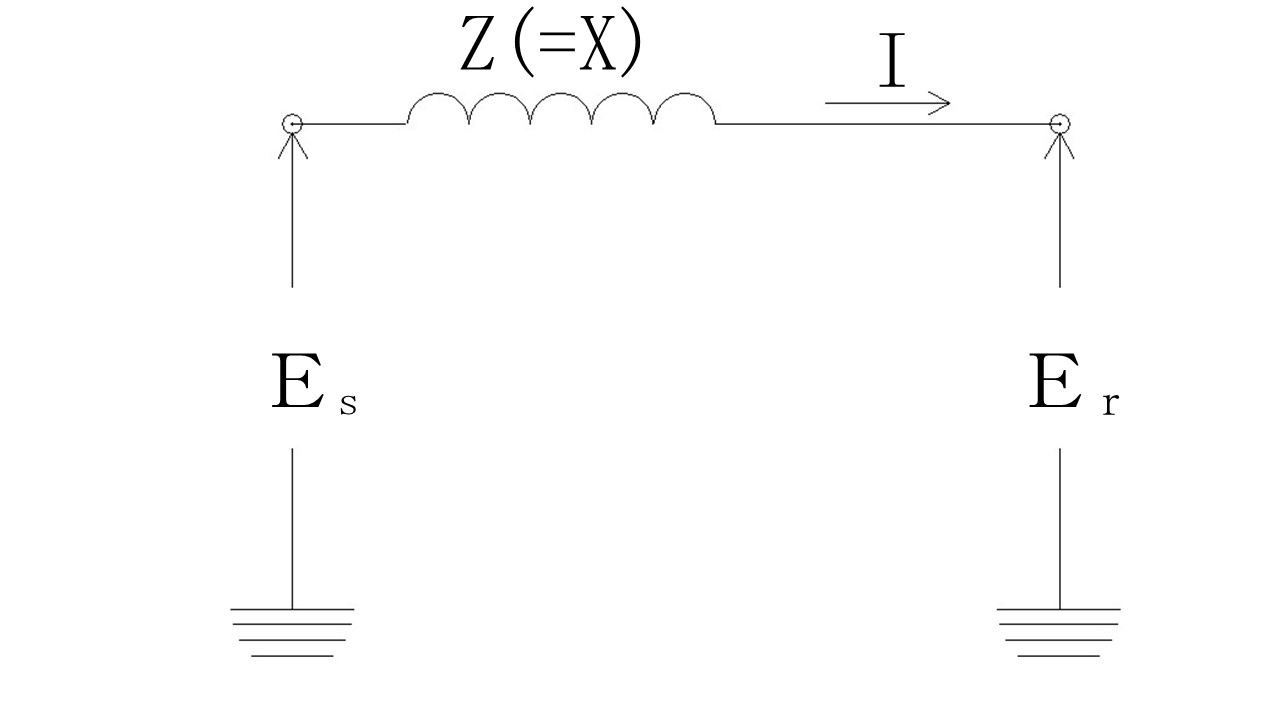
この問題を、図で表すと上の図になります。

これを、ベクトル図で表すと、上の図になります。
この図より、有効電力 $\sqrt{3}\ V_r\ I\ cos\theta$ を求めます。
受電端相電圧 $\dot{E}_r$ に電圧降下分の $\dot{X}\dot{I}$ を足すと送電端電圧 $\dot{E}_s$ になります。
その図に、三角形 $abc$ を書き加えています。
まずは、図より $bc$ について考えてみます。
$bc=\dot{E}_s\ sin\delta\ =\dot{X}\dot{I}\ cos\theta$ と書けます。
この式から、有効電力$\sqrt{3}\ \dot{V}_r\ \dot{I}\ cos\theta$ の $\dot{I}\ cos\theta$ を求めます。
$\dot{I}cos\theta=\cfrac{\dot{E}_s}{X}sin\delta$ となります。
上の有効電力の式 $\sqrt{3}V_r\ I\ cos\theta$ に $V_r=\sqrt{3}E_r$ を代入すると $3\ E_r\ I\ cos\theta$ となります。
ここに、$I\ cos\theta=\cfrac{E_s}{X}sin\delta$ を代入すると、
$\cfrac{3\ E_r\ E_s}{X}\ sin\delta$ となります。
ここで、答えに合わせるために、$\sqrt{3}E_r=V_r$ と $\sqrt{3}E_s=V_s$ を代入すると、
$\cfrac{V_s\ V_r}{X}sin\ \delta$ となります。
まとめ
電験二種の2次試験の電力・管理に出てくる問題に似ています。
電験二種では、もう少しひねっていますが。
送電端電圧と受電端電圧の関係を表す図は、よく覚えておいてください。
それと、送電端電圧=受電端電圧+電圧降下、の式もです。
割りと難しい問題だと思います。
解き方にも、テクニックが必要です。
よって、今はできなくても問題はないと思います。


コメント