問題
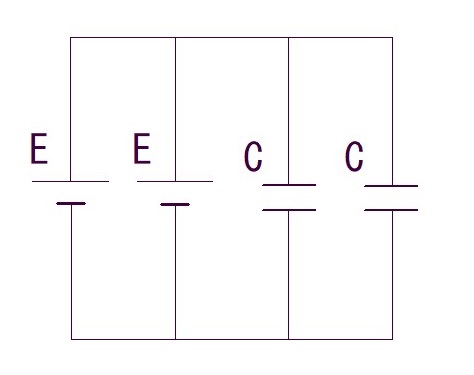
図に示す5種類の回路は、直流電圧E〔V〕の電源と静電容量C〔F〕のコンデンサの個数と組み合わせ異にしたものである。
これらの回路のうちで、コンデンサ全体に蓄えられている電界のエネルギーが最も小さい回路を示す図として、正しいのはどれか?
(1)
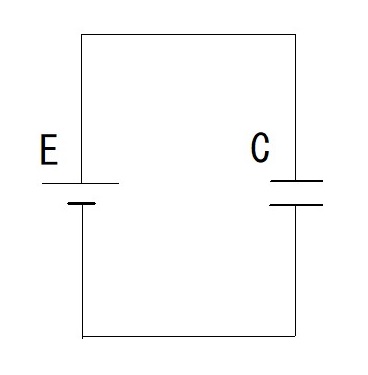
(2)
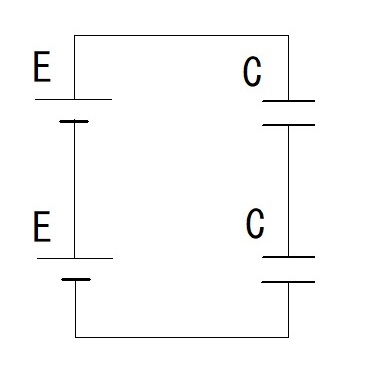
(3)
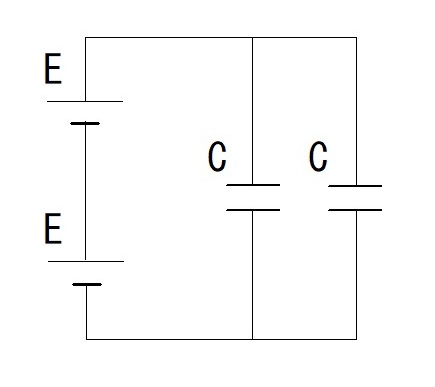
(4)
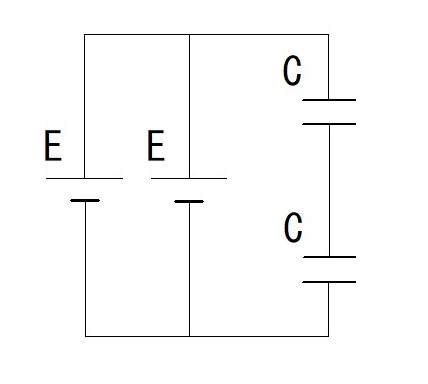
(5)
この問で必要な公式
公式① $W=\cfrac{1}{2}\ Q\ V$ 〔J〕
公式② $Q=C\ V$ 〔C〕
$W$ :エネルギー 〔J〕 $Q$ :電荷 〔C〕
$V$ :電圧 〔V〕 $C$ :静電容量 〔F〕
解答
正解は(4)です。
公式① $W=\cfrac{1}{2}\ Q\ V$ 〔J〕に、公式② $Q=C\ V$ 〔C〕を代入します。
$W=\cfrac{1}{2}(C\ V)\ V=\cfrac{1}{2}\ C\ V^2$ となります。
これを元に、(1)から数値を代入していきます。
(1)電圧は $E$ 〔V〕で、静電容量は $C$ 〔F〕となるので、
$W=\cfrac{1}{2}C\ E$ 〔J〕となります。
(2)電圧は $2E$ 〔V〕で、静電容量は直列なので $\cfrac{C\ \times\ C}{C+C}=\cfrac{C}{2}$ 〔F〕となるので、
$W=\cfrac{1}{2}\times\cfrac{C}{2}\times(2E)^2=CE^2$ 〔J〕となります。
(3)電圧は $2E$ 〔V〕で、静電容量は並列なので $C+C=2C$ 〔F〕となるので、
$W=\cfrac{1}{2}\times2C\times(2E)^2=4CE^2$ 〔J〕となります。
(4)電圧は並列なので $E$ 〔V〕そのままで、静電容量は直列なので$\cfrac{C\ \times\ C}{C+C}=\cfrac{C}{2}$ 〔F〕となるので、
$W=\cfrac{1}{2}\times\cfrac{C}{2}\ \times\ E^2=\cfrac{1}{4}CE^2$ 〔J〕となります。
(5)電圧は並列なので $E$ 〔V〕そのままで、静電容量は並列なので $C+C=2C$ 〔F〕となるので、
$W=\cfrac{1}{2}\times2C\ \times\ E^2=CE^2$ 〔J〕となります。
解説
平成21年度の理論問3に、コイルのエネルギーの問題が出ていました。
その時も、説明をするのに良いイメージが沸かず、お茶をにごしました。
今回も、すっきりとは行かないと思います。
では、始めます。
まず、公式① $W=\cfrac{1}{2}\ Q\ V$ 〔J〕の $\cfrac{1}{2}$ についてです。
エネルギーとは、「仕事をするための力」のことです。
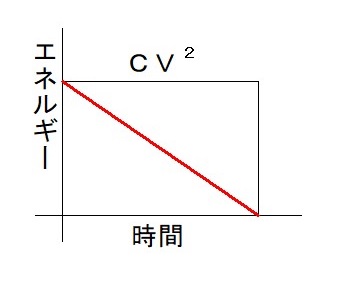
エネルギーが仕事をすると時間と共に減り、最終的には無くなります。赤線のごとくです。
よって、エネルギーの式には $\cfrac{1}{2}$ が付きます。
次に、下のどちらの式を基準に覚えておくか?
$W=\cfrac{1}{2}QV$ が良いか、$W=\cfrac{1}{2}CV^2$ が良いか?です。
今回は $W=\cfrac{1}{2}QV$ を基準としました。
その理由の一つ目は、$Q$ も $V$ も一次であるため、すっきりと見えること。
二つ目は、$W=V\ I$ 〔W〕(電力=電圧×電流)と結びつき易いことです。
$Q$ は電流の元の電荷です。電流の元に電圧 $V$ を掛けるとエネルギーになる。
電力の式をイメージできませんか?
これを、コイルのエネルギーで考えると、
$W=\cfrac{1}{2}\phi\ I$
$\phi$ :磁束〔Wb〕 $I$ :電流〔A〕
となります。
$\phi$ は発電機の電圧を生み出す元の磁束です。電圧の元と言えます。
電圧の元に、電流を掛けると、エネルギーになる。
こちらも、電力の式をイメージしやすいのではと思います。
コンデンサに蓄えられるエネルギーを考えるとき
公式① $W=\cfrac{1}{2}\ Q\ V$ 〔J〕を基準に
公式② $Q=C\ V$ 〔C〕で式変形をして
$W=\cfrac{1}{2}\ Q\ V\ =\cfrac{1}{2}\ C\ V^2=\cfrac{1}{2}\cfrac{Q^2}{C}$
を導き出す。
コイルのエネルギーの場合は、
$W=\cfrac{1}{2}\phi\ I$ 〔J〕を基準に、
$\phi=L\ I$ 〔Wb〕で式変形をして、
$W=\cfrac{1}{2}\phi\ I=\cfrac{1}{2}L\ I^2=\cfrac{1}{2}\cfrac{\phi^2}{L}$
を導き出す。
しかし欠点として、$W=\cfrac{1}{2}Q\ V$ と言う式は、あまり出てこないのです。
エネルギーの式として覚えておくなら、この問題で出てきている
$W=\cfrac{1}{2}C\ V^2$ が一般的です。
コイルのエネルギーの場合は、$W=\cfrac{1}{2}L\ I^2$ の形がほとんどです。
それに、コンデンサの場合、$W=\cfrac{1}{2}C\ V^2$ を導き出すために、
$W=\cfrac{1}{2}Q\ V$ と $Q=C\ V$ の二つを思い出して、
さらに、式変形をしないと、$W=\cfrac{1}{2}C\ V^2$ にたどり着けない。
時間の無い試験本番において、タイムロスも甚だしい気もします。
覚えやすい公式を覚える。
かつ、要らない公式は覚えない。
と思っている私としては、どちらが良いか悩むところです。
皆さんは、どちらが良いと思いますか?各自で考えてください。
(これだけすっきりしない話を読まされると、少しは記憶に残るのでは?と期待します。)
次に、コンデンサの並列接続と直列接続による静電容量の求め方についてです。
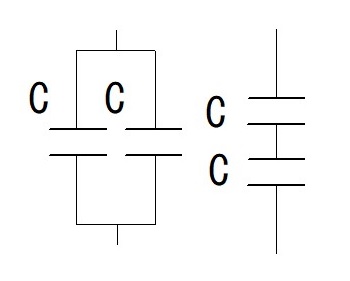
この図から何となくイメージできると思いますが、
並列接続の場合は、コンデンサの極板の面積が増える。
直列接続の場合は、コンデンサの極板間距離が増える。
静電容量は $C=\varepsilon\cfrac{S}{d}$ と表すことができます。
ここで、$\varepsilon$ が誘電率〔F/m〕、$S$ が面積〔m²〕、$d$ が極板間距離〔m〕です。
並列接続の時は、$C=C_1+C_2=\varepsilon\cfrac{S_1+S_2}{d}$ と計算できます。
直列接続の時は、$\cfrac{1}{C}=\cfrac{1}{C_1}+\cfrac{1}{C_2}=\cfrac{d_1+d_2}{\varepsilon\ S}$ より $C=\cfrac{\varepsilon\ S}{d_1+d_2}$ と計算できます。
(コンデンサが二つだけの直列接続の場合は、$\cfrac{\ 積\ }{\ 和\ }$ となります。
抵抗の並列接続の時にやったと思います。)
まとめ
この問題は、$W=\cfrac{1}{2}C\ V^2$ とコンデンサの並列接続と直列接続の静電容量の求め方の知識が必要です。
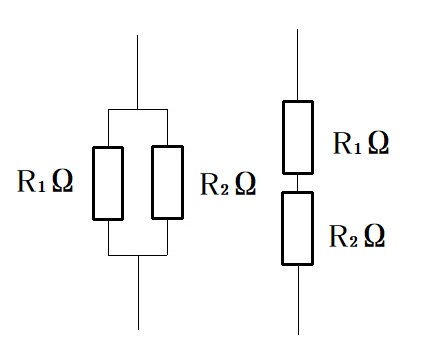
コンデンサの直列・並列接続の静電容量の求め方は、抵抗の直列・並列接続の求め方と反対ですので、すぐに覚えられると思います。
(静電容量は $C=\varepsilon\cfrac{S}{d}$ に対して、抵抗は、$R=\rho\cfrac{l}{S}$ となり、
静電容量と抵抗では、分母と分子が逆になっているので、
直列・並列接続の求め方が逆になります。)
後は、$W=\cfrac{1}{2}C\ V^2$ についてですが、コイルとコンデンサを対にして覚えておくと、少し楽になると思います。
オマケ
$W=\cfrac{1}{2}\ Q\ V$
「エネルギー( $W$ )はキューブ( $Q\ V$ )の半分( $\cfrac{1}{2}$ )」
意味のない語呂合わせでした。
コメント