問題
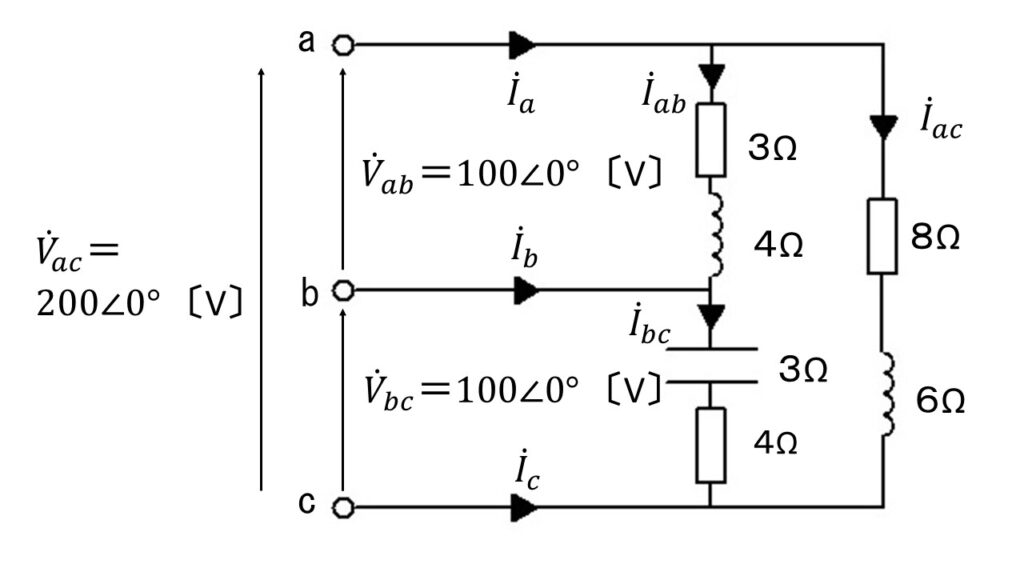
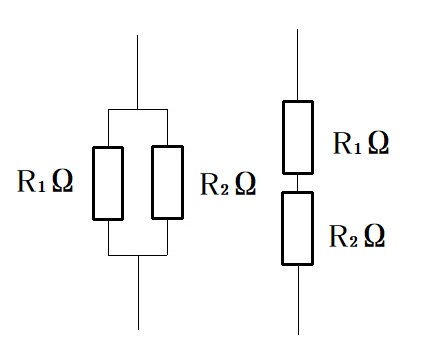
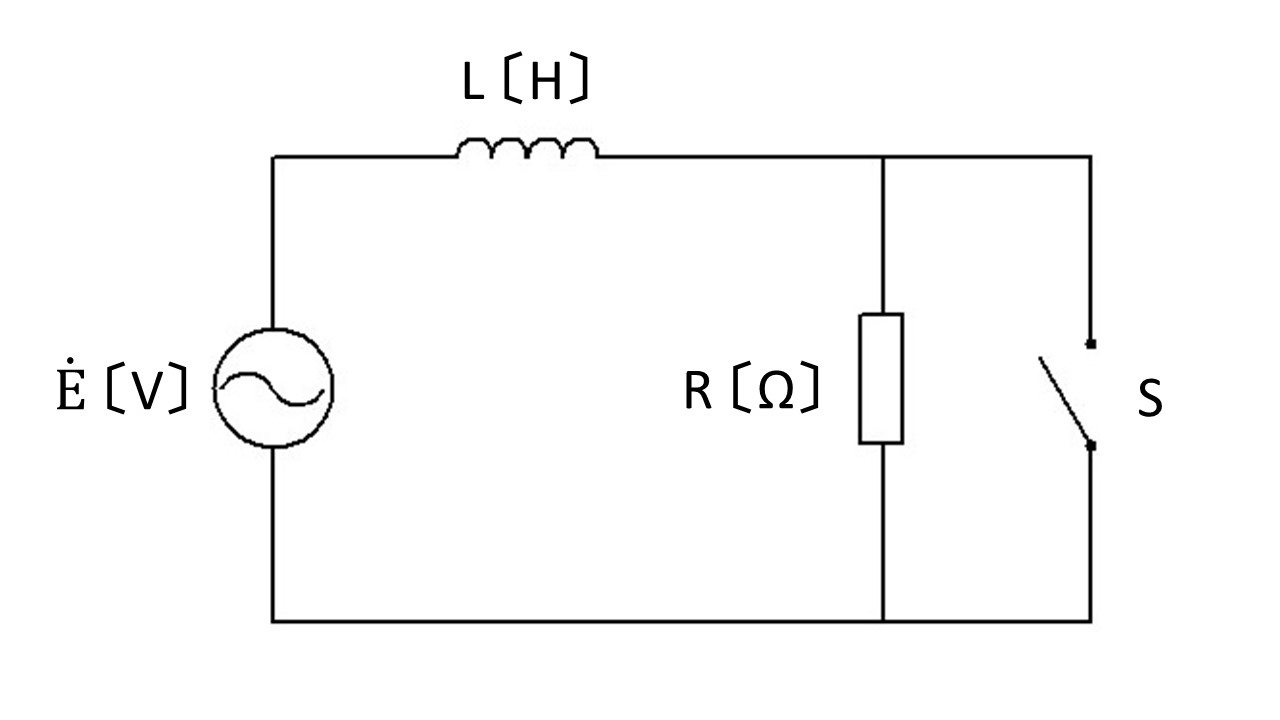
図のように抵抗、コイル、コンデンサからなる負荷がある。この負荷に線間電圧
$\dot{V}_{ab}=100\angle0^{\circ}$ 〔V〕、$\dot{V}_{bc}=100\angle0^{\circ}$ 〔V〕、$\dot{V}_{ac}=200\angle0^{\circ}$ 〔V〕、
の単相3線式交流電源を接続したところ、端子 $a$ 、端子 $b$ 、端子 $c$ を流れる電流はそれぞれ、
$\dot{I}_a$ 〔A〕、$\dot{I}_b$ 〔A〕、$\dot{I}_c$ 〔A〕であった。
$\dot{I}_a$ 〔A〕、$\dot{I}_b$ 〔A〕、$\dot{I}_c$ 〔A〕の大きさをそれぞれ $I_a$ 、$I_b$ 、$I_c$ としたとき、
これらの大小関係を表す式として正しいのはどれか。
(1) $I_a=I_c>I_b$
(2) $I_a>I_c>I_b$
(3) $I_b>I_c>I_a$
(4) $I_b>I_a>I_c$
(5) $I_c>I_a>I_b$
この問で必要な公式
① $\dot{I}=\cfrac{\dot{V}}{\dot{Z}}$
② $\dot{Z}=Z_R+jX_L-jX_C$
解答
正解は(2)
まず、$\dot{I}_{ab}$ を求めましょう。
a~b間のインピーダンス $\dot{Z}_{ab}$ は、公式②より
$\dot{Z}_{ab}=Z_R+jX_L=3+j4$ となります。
これを公式①に代入すると、
$\dot{I}_{ab}=\cfrac{\dot{V}_{ab}}{\dot{Z}_{ab}}=\cfrac{100\angle0^{\circ}}{3+j4}$
分母の虚数を消す( $j$ を取る)ために、分母・分子に $3-j4$ を掛けると、
$\cfrac{100\angle0^{\circ}\times(3-j4)}{(3+j4)(3-J4)}=\cfrac{100(3-j4)}{3^2+4^2}=\cfrac{300-j400}{25}=12-j16$
となります。
次に、$\dot{I}_{bc}$ を求めましょう。
b~c間のインピーダンス $\dot{Z}_{bc}$ は、公式②より
$\dot{Z}_{bc}=Z_R-jX_C=4-j3$ となります。
これを公式①に代入すると、
$\dot{I}_{bc}=\cfrac{\dot{V}_{bc}}{\dot{Z}_{bc}}=\cfrac{100\angle0^{\circ}}{4-j3}$
分母の虚数を消す( $j$ を取る)ために、分母・分子に $4+j3$ を掛けると、
$\cfrac{100\angle0^{\circ}\times(4+j3)}{(4-j3)(4+J3)}=\cfrac{100(4+j3)}{4^2+3^2}=\cfrac{400+j300}{25}=16+j12$
となります。
次は、当然、$\dot{I}_{ac}$ を求めましょう。
a~c間のインピーダンス $\dot{Z}_{ac}$ は、公式②より
$\dot{Z}_{ac}=Z_R+jX_L=8+j6$ となります。
これを公式①に代入すると、
$\dot{I}_{ac}=\cfrac{\dot{V}_{ac}}{\dot{Z}_{ac}}=\cfrac{200\angle0^{\circ}}{8+j6}$
分母の虚数を消す( $j$ を取る)ために、分母・分子に $8-j6$ を掛けると、
$\cfrac{200\angle0^{\circ}\times(8-j6)}{(8+j6)(8-J6)}=\cfrac{200(8-j6)}{8^2+6^2}=\cfrac{1600-j1200}{100}=16-j12$
となります。
求めたいのは、$I_a$ 、$I_b$ 、$I_c$ です。
$\dot{I}_a$ は、図から分かるように、$\dot{I}_a=\dot{I}_{ab}+\dot{I}_{ac}$ となります。
上で求めた値を代入すると、
$\dot{I}_a=12-j16+16-j12=28-j28$
となります。
よって、$I_a=\mid \dot{I}_a\mid=\sqrt{28^2+28^2}=28\sqrt{2}\fallingdotseq 39.598$
となります。
$\dot{I}_b$ は、$\dot{I}_{bc}-\dot{I}_{ab}$ になります。
数値を代入すると、
$\dot{I}_b=16+j12-(12-j16)=4+j28$
となります。
よって、$I_b=\mid \dot{I}_b\mid=\sqrt{4^2+28^2}=\sqrt{800}\fallingdotseq 28.284$
となります。
$\dot{I}_c$ は、$-\dot{I}_{bc}-\dot{I}_{ac}$ になります。
数値を代入すると、
$\dot{I}_c=-16-j12-(16-j12)=-32$
となります。
よって、$I_c=\mid \dot{I}_c\mid=\mid -32 \mid=32$
となります。
以上により、求める $I_a$ 、$I_b$ 、$I_c$ は、
それぞれ 39.598〔A〕、28.284〔A〕、32〔A〕となります。
大小関係は、(2) $I_a>I_c>I_b$ となります。
解説
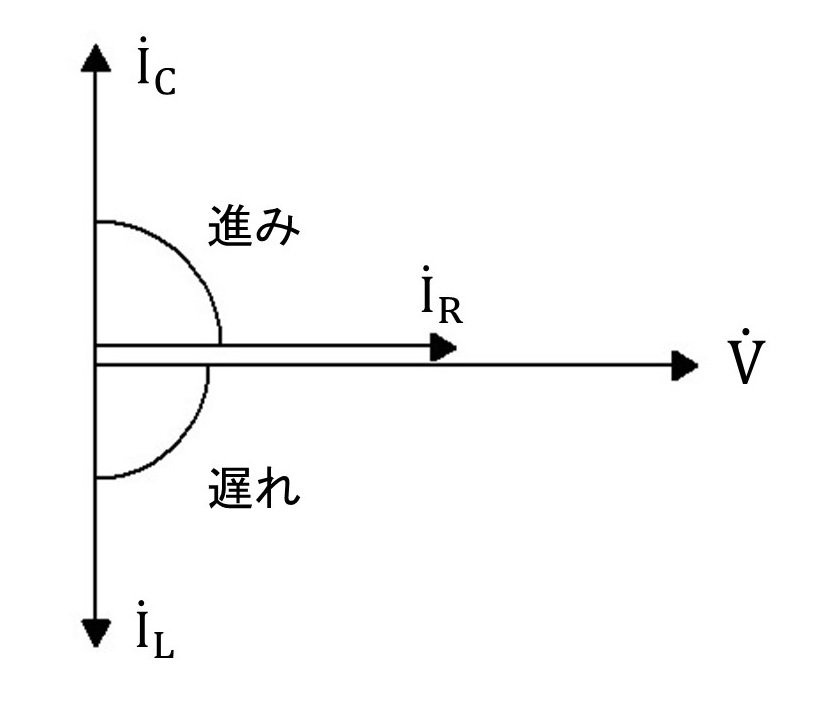
電圧に対して、電流が進んでいるか、遅れているか、又は同相かを示す図です。
よく見かける図だと思います。このまま覚えましょう。
3種では、電流が遅れる進むの導出過程を覚える必要がないのですが、一応、説明しておきます.
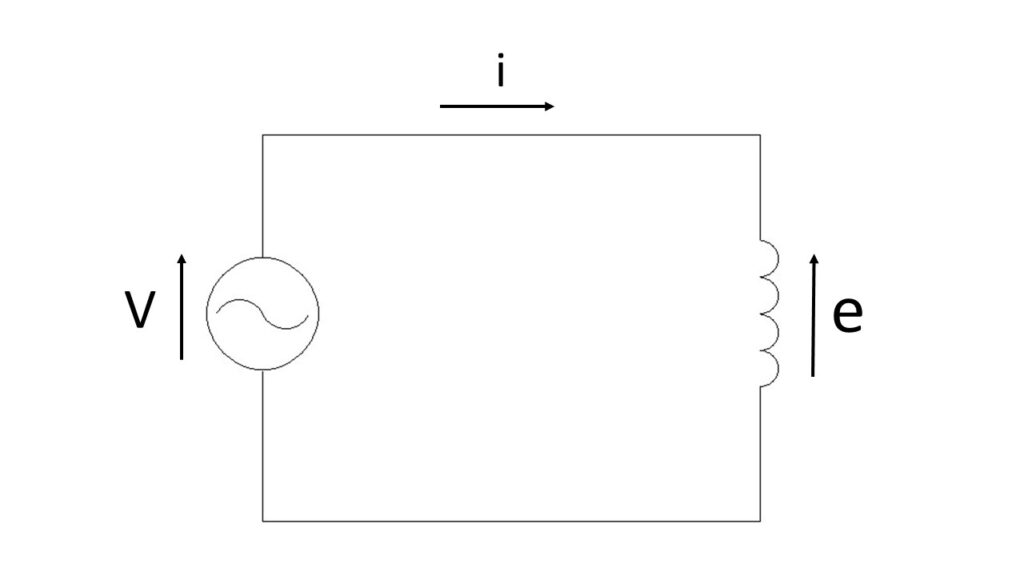
コイルの場合は、電源電圧を $v$ 、誘導起電力を $e$ 、電流を $i$ とすると
誘導起電力 $e$ は電流の変化を妨げる方向に発生するので、インダクタンス $L$ として、
$e=-L\cfrac{di}{dt}$ となります。
また、$e=-v$ より、$v=L\cfrac{di}{dt}$ と表せます。
ここで、$i$ は交流の瞬時値であるので、$i=I_m\ sin\ \omega\ t$ とおくと
$v=L\ I_m\cfrac{d\ sin\ \omega\ t}{dt}=L\ I_m\ \omega\ cos\ \omega\ t$ となります。
$cos\ \theta=sin(\theta\ +\ \cfrac{\pi}{2})$ と表せることから、
$v=L\ I_m\ \omega\ sin(\omega\ t\ +\ \cfrac{\pi}{2})$ となります。
これは、電流 $i$ が $sin\ \omega\ t$ に対して、電圧 $v$ は $sin(\omega\ t\ +\ \cfrac{\pi}{2})$ となることから、電圧は電流に対して $\cfrac{\pi}{2}=90^\circ$ 進んでいると言えます。
電圧基準で見れば、電流は電圧に対して$\cfrac{\pi}{2}=90^\circ$ 遅れていると言うことです。
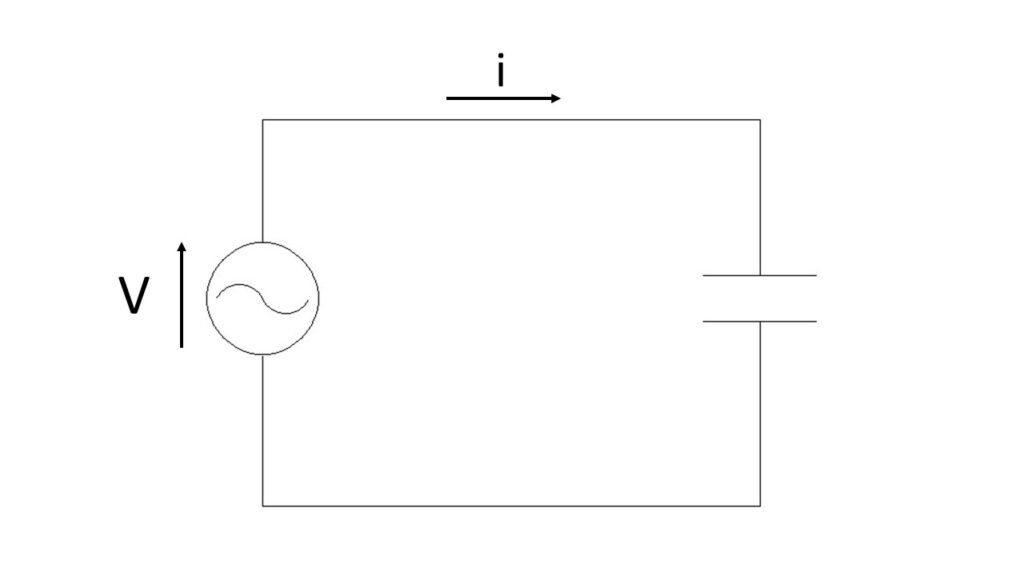
コンデンサの場合は、電源電圧を $v$、電流を $i$ とすると、
まず、電流 $i$ はコンデンサに流れ込む電荷のことですから、$i=\cfrac{dQ}{dt}$ と書けます。
ここで、$Q=C\ v$ となることから、$i=\cfrac{d(C\ v)}{dt}=C\cfrac{dv}{dt}$ となります。
$v$ は交流の瞬時値であるので、$v=V_m\ sin\ \omega\ t$ とおくと、
$i=C\cfrac{d(\ V_m\ sin\ \omega\ t)}{dt}=C\ V_m\cfrac{d\ sin\ \omega\ t}{dt}=C\ V_m\ \omega\ cos\ \omega\ t$ となります。
コイルの時と同様に $cos$ を $sin$ に直して、$i=C\ V_m\ \omega\ sin(\omega\ t\ +\ \cfrac{\pi}{2})$ となります。
これは、電圧 $v$ が $sin\ \omega\ t$ に対して、電流 $i$ は $sin(\omega\ t\ +\ \cfrac{\pi}{2})$ となることから、電流は電圧に対して $\cfrac{\pi}{2}=90^\circ$ 進んでいると言えます。
これを簡単に、微分を使わずに説明しているところが見つからないのでこの辺で。
コイルは電流が遅れるのは、上の説明で分かったことにしておきましょう。
コイルの電流が電圧に対して遅れるのか進むのか、迷ったときのために他のアプローチを。
「電力」の問題で、「遅れ力率0.8とする」というのをよく見かけると思います。
「進み力率」という言葉を問題の中に見ることは、ほぼ稀です。
なぜならば、一般の家庭や工場など、電気を使っている所は、まず遅れ力率だからです。
今、電気に仕事をさせようとすれば、モーターに仕事をさせるのがほとんどです。
冷蔵庫やエアコンで温度を上げ下げするためのヒートポンプに使われる空気圧縮機もモーターを使っています。
洗濯機やエレベーター、エスカレーター然り。ベルトコンベア然りです。
で、モーターはコイルからできています。
世の中は、コイル負荷があふれていて、遅れ力率で運用されている。
というのが、何となく分かっていただけたでしょうか。
さらにもう一つ、電力の問題に出てくる「進相コンデンサ」と言う言葉です。
遅れ無効電力を打ち消すために、進み無効電力を供給するコンデンサのことです。
コンデンサは相を進ませるので、「進相コンデンサ」と言われているのです。
これで、コイルは電流が遅れで、コンデンサは電流が進み、と言うのを覚えていただけたでしょうか?
まとめ
この問は、交流電源に抵抗、コイル、コンデンサの各負荷をつないだ時の、電流の大きさを求めるものです。
インピーダンスを複素数表示(虚数を使って表示)し、オームの法則により電流を求めます。
分母に虚数が含まれている場合は、分母の虚数を消します。
その時に使うのが、共役複素数です。
(解答で、分母分子に掛けていたものです。)
共役複素数とは、ある複素数の虚数の符号を($j$ の前の符号を)変えた複素数です。
$(a+b)(a-b)=a^2-b^2$ という2次式を昔習ったとは思います。
これを複素数に応用すると、$(a+jb)(a-jb)=a^2+b^2$ となり、$j$ が消えます。
分母に細工をすれば、分子にも同じことしないと分数が壊れてしまいますよね。
だから、「分母の共役複素数を分母分子に掛ける。」ってなります。
ついでに、$I$ の大きさを求めるときに使用した定理が「三平方の定理」ですよね。
名前を忘れている人がいると思ったので、書いておきました。
問題の解き方は、定型化されたものです。
複素数に慣れておいてください。
反省
計算問題の解説なのに、だらだらとした説明になってしまいました。
ごめんなさい。
コメント