問題
次の文章は、コイルの磁束鎖交数とコイルに蓄えられる磁気エネルギーについて述べたものである。
インダクタンス1〔mH〕のコイルに直流電流10〔A〕が流れているとき、このコイルの磁束鎖交数 $\Psi_1$ 〔Wb〕は ( ア ) 〔Wb〕である。また、コイルに蓄えられている磁気エネルギー $W_1$ 〔J〕は ( イ ) 〔J〕である。
次にコイルに流れる直流電流を30〔A〕とすると、磁束鎖交数 $\Psi_2$ 〔Wb〕と蓄えられている磁気エネルギー $W_2$ 〔J〕はそれぞれ ( ウ ) となる。
1 (ア)$5\times10^{-3}$ (イ)$5\times10^{-2}$
(ウ)$\Psi_2$ は $\Psi_1$ の3倍、$W_2$ は $W_1$ の9倍
2 (ア)$1\times10^{-2}$ (イ)$5\times10^{-2}$
(ウ)$\Psi_2$ は $\Psi_1$ の3倍、$W_2$ は $W_1$ の9倍
3 (ア)$1\times10^{-2}$ (イ)$1\times10^{-2}$
(ウ)$\Psi_2$ は $\Psi_1$ の9倍、$W_2$ は $W_1$ の3倍
4 (ア)$1\times10^{-2}$ (イ)$5\times10^{-1}$
(ウ)$\Psi_2$ は $\Psi_1$ の3倍、$W_2$ は $W_1$ の9倍
5 (ア)$5\times10^{-2}$ (イ)$5\times10^{-1}$
(ウ)$\Psi_2$ は $\Psi_1$ の9倍、$W_2$ は $W_1$ の27倍
この問で必要な公式
① $\Psi\ =\ L\ I$ 〔Wb〕
② $W\ =\ \cfrac{1}{2}\ L\ I^2$ 〔J〕
$\Psi$ :磁束鎖交数 〔Wb〕 $L$ :インダクタンス 〔H]
$I$ :電流 〔A〕 $W$ :磁気エネルギー 〔J〕
解答
正解は、2番
(ア) ①式に数値を代入します。
磁束鎖交数 $\Psi$ 〔Wb〕は、インダクタンス $L=1\times10^{-3}$ 〔H〕と電流 $I=10$ 〔A〕の積となるので、$$\Psi=1\times10^{-3}\times10\ =1\times\ 10^{-2}$$ となります。
(イ) ②式に数値を代入します。
コイルに蓄えられるエネルギー $W$ は、インダクタンス $L=1\times10^{-3}$ 〔H〕と電流の2乗 $I^2=10^2$ 〔A²〕の積の $\cfrac{1}{2}$ となるので、$$W=\cfrac{1}{2}\times1\times10^{-3}\times10^2=\cfrac{1}{2}\times1\times10^{-1}=5\times10^{-2}$$ となります。
(ウ) 電流を10〔A〕から30〔A〕へと、3倍に増やした場合、
磁束鎖交数 $\Psi$ は $\Psi=L\times(3I)=3LI=3\Psi$ となり、
元の3倍となります。
次に、コイルに蓄えられるエネルギーWは、$W=\cfrac{1}{2}L(3I)^2=9\cfrac{1}{2}LI^2=9W$ となり、
元の9倍となります。
解説
公式① $\Psi\ =\ L\ I$ 〔Wb〕についてですが、
磁束鎖交数 $\Psi$ 〔Wb〕は、あるコイルに電流 $I$ (A〕を流した時に発生する磁束の総数のことです。
では、インダクタンス $L$ 〔H〕は、、、、そうです、比例定数です。
コイルは、その形状や巻き数により発生する磁束の総数(磁束鎖交数)が変わってきます。
だから各コイルが持つ「固有の比例定数」が必要であり、それがインダクタンス $L$ です。
次に、公式② $W\ =\ \cfrac{1}{2}\ L\ I^2$ 〔J〕についてです。
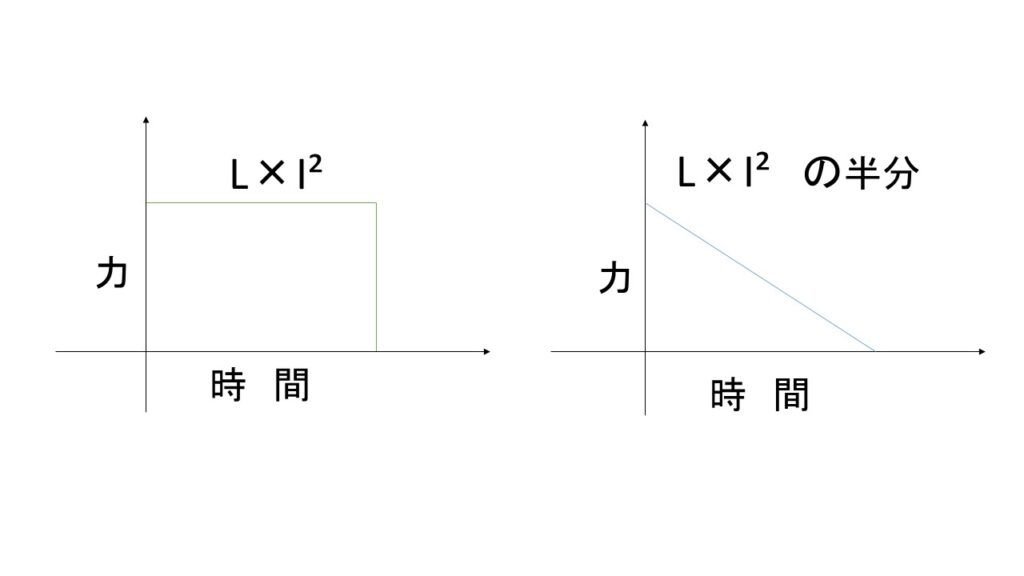
エネルギーの公式には、よく $\cfrac{1}{2}$ が付きます。
これは、エネルギーの元となる力が時間と共に減少し、やがて0になってしまうためです。
ただ、 $L\ \times\ I^2$ の $I^2$ がスッキリと説明できません。
(時間で積分すれば、どうのこうのと言うと面倒ですのでパスします。)
どこかで、すっきりと説明をしているサイトを見つけたら、拝借しお披露目します。
閑話休題、ここでコンデンサと見比べてみましょう。
コンデンサのエネルギーの元となっているのが電荷 $Q$ です。
$Q$ を表す式は、$Q=CV$ となります。
ここに $V$ と $\cfrac{1}{2}$ を掛けてあげると、エネルギー $W=\cfrac{1}{2}CV^2$ となります。
次に、コイルのエネルギーの元となっているのが磁束鎖交数 $\Psi$ です。
$\Psi$ を表す式は、$\Psi=LI$ となります。
ここに $I$ と $\cfrac{1}{2}$ を掛けてあげると、エネルギー $W=\cfrac{1}{2}LI^2$ となります。
似ていますね。間違えないようにしてください。
コンデンサの電荷 $Q$ は電流の元です。なのに、エネルギーになると電圧 $V^2$ と組みます。
コイルの磁束鎖交数 $\Psi$ は、発電機の電圧を発生さする元です。なのに、エネルギーになると電流 $I^2$ と組みます。
アマノジャクですね。くれぐれも間違わないようにしてください。
スッキリした説明が思い付かない(見つからない)ので、お茶を濁しました。
ひとこと
「コンデンサ」と「コイル」、「C」と「L」は対をなすことが多いので、公式を書きだして見比べて見るのも面白いですよ。
また、静電気と磁気も似たような公式が多々ありますので、見比べて見てください。
まとめ
この問は、公式に数値を入れていくタイプの問題です。
公式を覚えておくことは当然として、次に単位にも注意しましょう。
皆さんもやっているとは思いますが、例えばこの問題だと〔mH〕がでてきます。
ミリと出てくれば,ちゃんと( $\times\ 10^{-3}$ )と別口に式の中に落とし込みましょう。
計算間違いが、少しは減るのではないでしょうか?
コメント