問題
ある回路に、$i=4\sqrt{2}sin120\pi t$ 〔A〕の電流が流れている。この電流の瞬時値が、時刻 $t=0$ 〔s〕以降に初めて $4$ 〔A〕となるのは、時刻 $t=t_1$ 〔s〕である。
$t_1$ 〔s〕の値として、正しいのどれか?
(1) $\cfrac{1}{480}$ (2) $\cfrac{1}{360}$ (3)$\cfrac{1}{240}$
(4) $\cfrac{1}{160}$ (5) $\cfrac{1}{120}$
この問で必要な公式
① 交流の電圧、電流の瞬時値=$A_msin\ \omega\ t$
$A_m$ =最大値 $\omega$=各速度〔rad〕($\omega=2\ \pi\ f$)
解答
正解は(1)です。
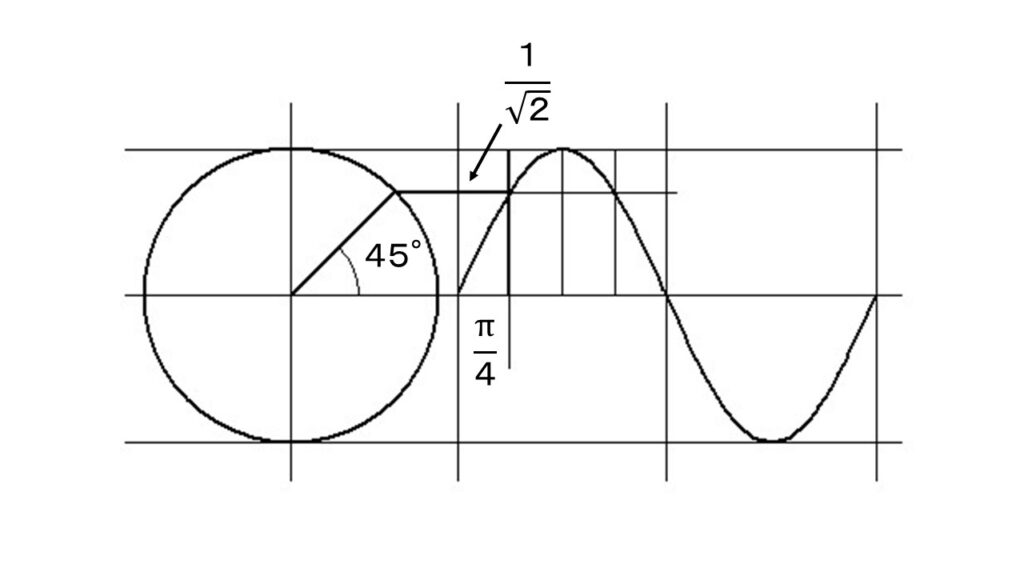
電流の瞬時値が、$i=4\sqrt{2}sin120\pi t$ で表されているとき、
最大値は $4\sqrt{2}$ です。
初めて4〔A〕となるのは、$4\sqrt{2}\times\cfrac{1}{\sqrt{2}}=4$ より、
上の図では、$\cfrac{1}{\sqrt{2}}$ の時であり、
45°進んだ時であり、
$\cfrac{\pi}{4}$ の時です。
1秒間に $120\pi$ 進む電流が、最初に $\cfrac{\pi}{4}$ に到達する時間は、
$\cfrac{1}{120\times4}=\cfrac{1}{480}$ になります。
式で見ていきましょう。
電流の瞬時値 $i=4\sqrt{2}sin120\pi t$ が4〔A〕とは、
$4\sqrt{2}sin120\pi t=4$ 〔A〕と表せます。
両辺を4で割って、$\sqrt{2}sin120\pi t=1$
両辺を $\sqrt{2}$ で割って、$sin120\pi t=\cfrac{1}{\sqrt{2}}$
ここで、$sin\theta=\cfrac{1}{\sqrt{2}}$ とすると、
$\theta=45^\circ=\cfrac{\pi}{4}$ です。
よって、$sin120\pi t=\cfrac{1}{\sqrt{2}}=sin\cfrac{\pi}{4}$ となります。
$sin$ の中を比べると、$120\pi t=\cfrac{\pi}{4}$ と書けるので、
$t=\cfrac{1}{4\times120}=\cfrac{1}{480}$ となります。
解説
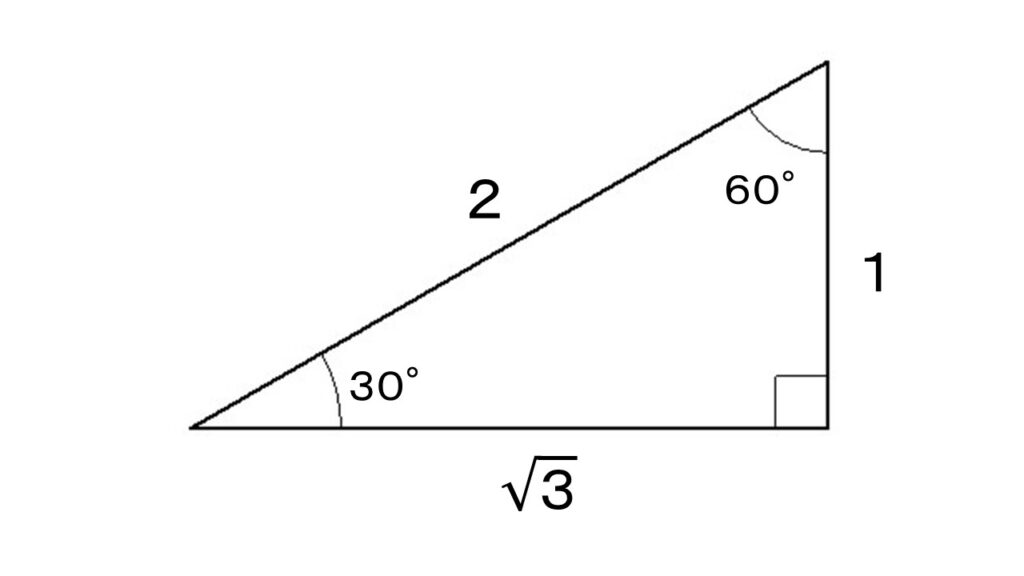
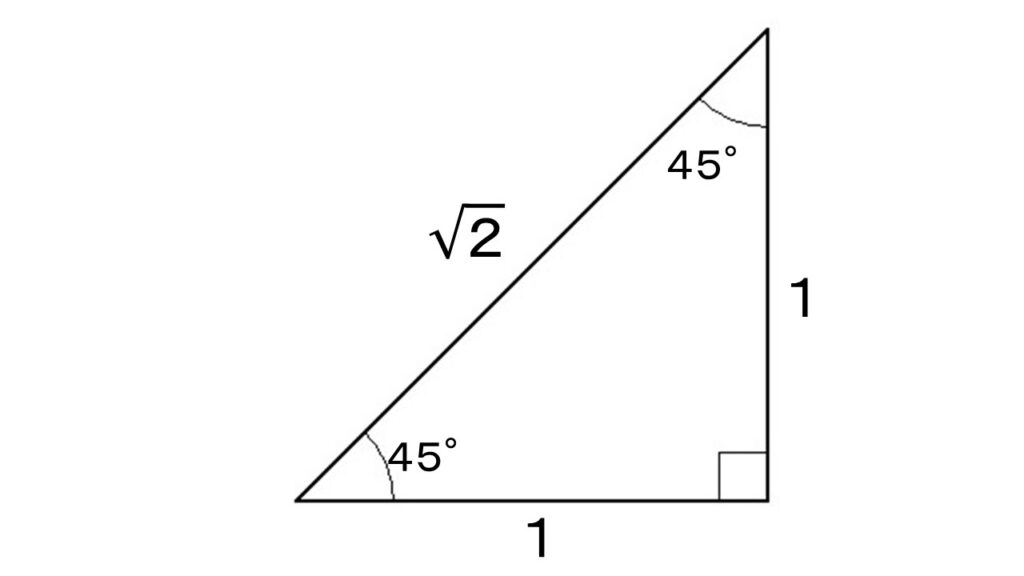
この二つの三角形から導き出せる $sin\ \ cos\ \ tan$ は覚えておきましょう。
$sin0^\circ=0$ 、 $sin30^\circ=\cfrac{1}{2}$
$sin45^\circ=\cfrac{1}{\sqrt{2}}$ 、 $sin60^\circ=\cfrac{\sqrt{3}}{2}$
$sin90^\circ=1$
$cos0^\circ=1$ 、 $cos30^\circ=\cfrac{\sqrt{3}}{2}$
$cos45^\circ=\cfrac{1}{\sqrt{2}}$ 、 $cos60^\circ=\cfrac{1}{2}$
$cos90^\circ=0$
$tan30^\circ=\cfrac{1}{\sqrt{3}}$ 、 $tan45^\circ=1$
$tan60^\circ=\sqrt{3}$
以上です。これくらいは、少し考えたら出てくるようにしておきましょう。
(上の二つの三角形の辺の比を覚えておけば、すぐに出てきます。)
解答の最初の図(電流の瞬時値を説明しようとして出した図)を少し説明します。
〔rad〕表記のとき、$\pi$ は半周で、一周は $2\pi$ です。
図は、一周( $2\pi$ )分の $sin$ 曲線を表示しています。
今回の問題で出てくる $4\sqrt{2}sin120\pi t$ という式は、
電流の瞬時値を表す式であることは、解答欄に書きました。
$4\sqrt{2}$ が最大値であることも、書きました。
$sin120\pi t$ は、1秒間に $120\pi$ 分だけ回転することです。
$2\pi$ で1周ですので、1秒間に60周回転する。
これは、60〔Hz〕ということです。
各速度 $\omega=2\pi f$ という公式を見たことがあると思います。
それも、ここからきています。
まとめ
冷静に考えれば、何となく分かる問題だと思います。
解答で使用した図を思い出しながら、じっくりと考えてください。
サービス問題だと思います。
コメント