問題
静電界に関する記述である、次のうち正しいのはどれか。
(1) 二つの小さな帯電体の間に働く力の大きさは、それぞれの帯電体の電気量の和に比例し、その距離の2乗に反比例する。
(2) 点電荷が作る電界は点電荷の電気量に比例し、距離に反比例する。
(3) 電気力線上の任意の点での接線の方向は、その点の電界の方向に一致する。
(4) 等電位面上の正電荷には、その面に沿った方向に正のクーロン力が働く。
(5) コンデンサの電極板間にすき間なく誘電体を入れると、静電容量と電極板間の電界は、誘電体の誘電率に比例して増大する。
この問で必要な公式
① $F=\cfrac{Q_1\ Q_2}{4\ \pi\ \varepsilon\ r^2}$ 〔N〕
② $E=\cfrac{Q}{4\ \pi\ \varepsilon\ r^2}$ 〔V/m〕
③ $C=\varepsilon\:\cfrac{S}{d}$ 〔F〕
④ $V=E\ d$ 〔V〕 式を変形すると $E=\cfrac{V}{d}$ 〔V/m〕
F:働く力 〔N〕 ℚ:電荷(帯電体の電気量) 〔C〕 $\varepsilon$ :誘電率 〔F/m〕
r:距離 〔m〕 C:静電容量 〔F〕 S:面積 〔m²〕
d:間隔 〔m〕
解答
正解は(3)です。
(1) 言葉が聞きなれないので、何を言っているのか悩んでしまうかも。
帯電体は、電荷を持った物体。電気量とは電荷のことです。
働く力は公式① $F=\cfrac{Q_1\ Q_2}{4\ \pi\ \varepsilon\ r^2}$ による。よって、「それぞれの帯電体の電気量の和に比例し」ではなく、「それぞれの帯電体の電気量の積に比例し」です。
(2) 「点電荷が作る電界」電界の強さは、公式② $E=\cfrac{Q}{4\ \pi\ \varepsilon\ r^2}$ のことです。
この式によると、「距離に反比例する」ではなく、「距離の2乗に反比例する」となります。
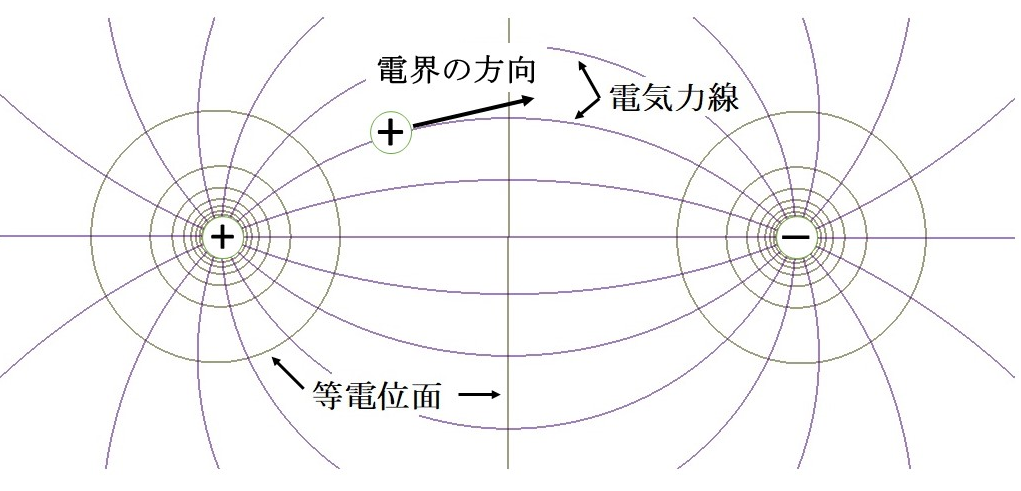
(3) 上の図のように電界の方向とは、たとえば自由に動ける「正の電荷」をその電場に置いたときに、その「正の電荷」が動く方向(クーロン力の方向)であり、電気力線の方向でもある。また、その電気力線が曲がっているときは、接線の方向がその点の電界の方向となります。
(4)(3)で説明しましたが、等電位面上の正電荷には、「その面に沿った」ではなく「その面と垂直な」方向に電気力線が走り、電気力線の方向にクーロン力が働きます。だから「その面と垂直な」方向に正の電荷が動くことになります。
(5)コンデンサについての問題です。まず、静電容量Cは公式③ $C=\varepsilon\:\cfrac{S}{d}$ より、たしかに誘電率 $\varepsilon$ に比例しています。しかし、電極板間の電界は公式④ $V=E\ d$ 式を変形すると $E=\cfrac{V}{d}$ より、誘電率 $\varepsilon$ とは無関係です。
解説
問題(1)及び(2)についてですが、
二つの電荷の間に働く力は、公式① $F=\cfrac{Q_1\ Q_2}{4\ \pi\ \varepsilon\ r^2}$ 〔N〕となります。これは、$Q_1$ の作り出す電界から $Q_2$ が受ける力ともいえます。
これを式で見ると、$F=\cfrac{Q_1\ Q_2}{4\ \pi\ \varepsilon\ r^2}=Q_2\cfrac{Q_1}{4\ \pi\ \varepsilon\ r^2}=Q_2\ E_1$ となります。
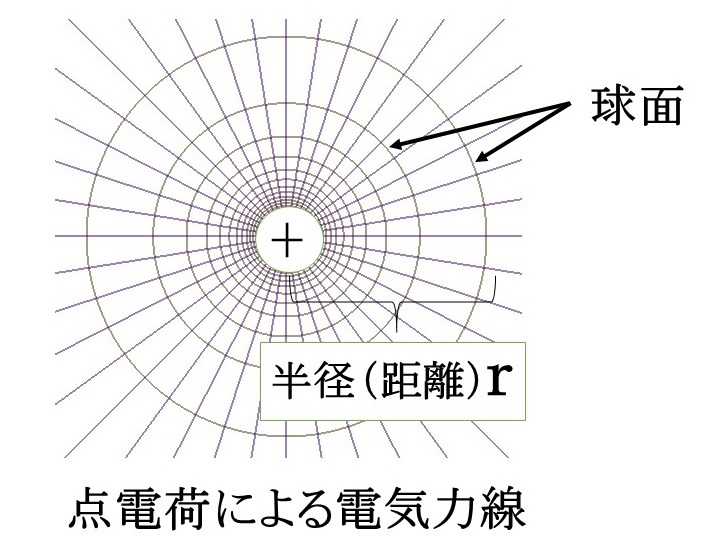
ここで、公式② $E=\cfrac{Q}{4\ \pi\ \varepsilon\ r^2}$ 〔V/m〕の説明から。
Qクーロンの点電荷から、$\cfrac{Q}{\varepsilon}$ 本の電気力線が出ていると定義されています。
また、Qクーロンの点電荷から距離 $r$ の点の電界の強さをEとして、その $r$ を半径とする球の表面積をSとします。また、電界の強さEは電気力線密度とも言えるので、電気力線の数は $E\ S$ とも表せます。
ここで球の表面積Sは $4\ \pi\ r^2$ であるので、代入して $4\ \pi\ r^2\ E=\cfrac{Q}{\varepsilon}$ となります。
これを式変形して、公式② $E=\cfrac{Q}{4\ \pi\ \varepsilon\ r^2}$ となります。
ここで、前の説明の逆をたどれば、公式① $F=\cfrac{Q_1\ Q_2}{4\ \pi\ \varepsilon\ r^2}$ 〔N〕となります。
問題(3)及び(4)は、解答の図を見てイメージしてください。
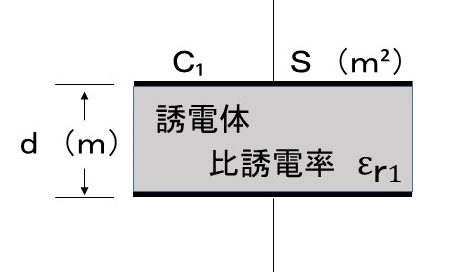
問題(5)に出てくる、静電容量Cは公式③ $C=\varepsilon\:\cfrac{S}{d}$ 〔F〕によります。
$C=\cfrac{\varepsilon\ S}{d}$ と書くと分かりやすいかと思います。
平成21年 問1にも出てくる公式ですが。少し変わった説明(覚え易い様なイメージを作成して)したいと思います。
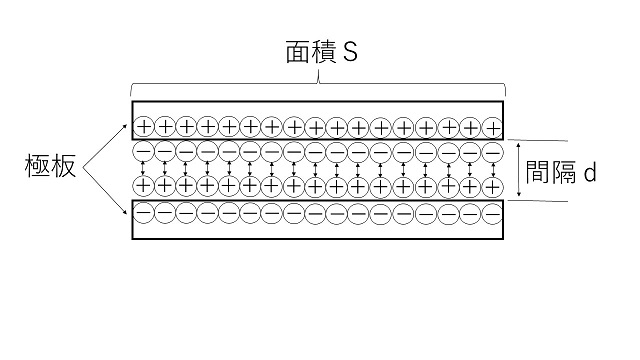
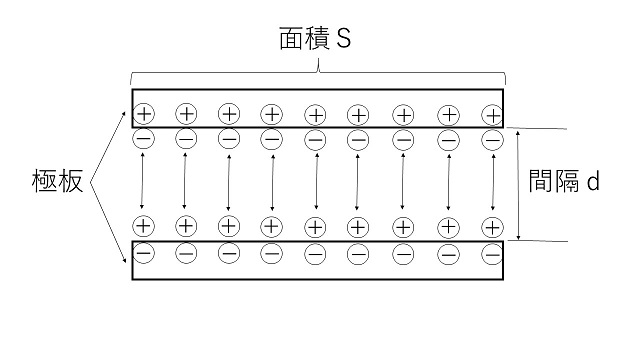
誘電率 $\varepsilon$ は、電極分離の係数だそうです。ここでは、これを平たく言えば、誘電体の中に̟⊕と̠⊖の電荷をどれだけ生み出せるか、の係数としましょう。
この値 $\varepsilon$ が大きくなれば極板に集まる電荷も多くなります。よって、静電容量Cも大きくなります。
また、面積Sが大きくなると、溜める面積が増えるので溜まる電荷も増えます。よって、静電容量Cも大きくなります。
その代わりに距離(間隔)dに反比例します。
これを、上の二つの図で説明します。まず、極板間の誘電体(この図では空気になりそうです。そこまで考えずに作っています。)の中で作られた電荷を極板付近に保持する力を仮定します。
この保持力は、+の極板に集まった⊖の電荷一つに対して、-の極板に集まった⊕の電荷一つが組になって存在する、その「絆」に由来するとしましょう。
間隔dが小さい(狭い)と「絆」が強く電荷が多く存在し、間隔dが大きいと「絆」が弱くなり電荷の数が減ってきます。
次に、コンデンサの電極板間の電界Eは、公式④ $V=E\ d$ 〔V〕 式を変形すると $E=\cfrac{V}{d}$ 〔V/m〕によります。
これも 平成21年 問1にも出てくる公式ですので、そのコピペになります。
ここに出てくる電界の強さEは、別名を電位の傾きと言います。下図のようなイメージです。
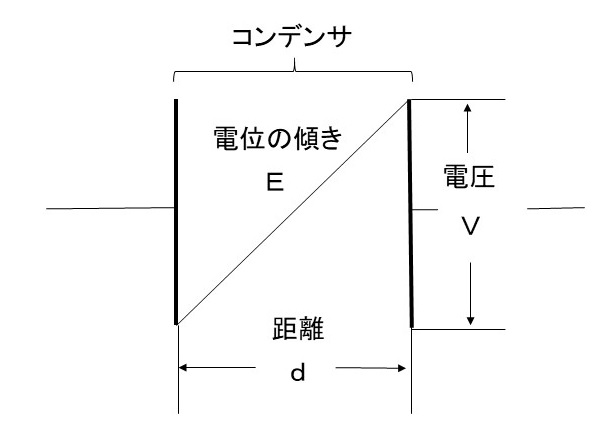
$y=ax$ の $a$ が傾きを表すのと同様に、$V=Ed$ の $E$ が傾きを表します。
ここに、$\varepsilon$ は出てきません。
まとめ
文章問題ですね。落ち着いて、よく読む。これに限ります。
問われている文章から、公式や図面を思い出す。
2乗があるのかないのか?
比例なのか、反比例なのか?
そもそも、その言葉の意味は?
緊張する試験の中ではありますが、落ち着いて、よく読む、としか言えません。
コメント