問題
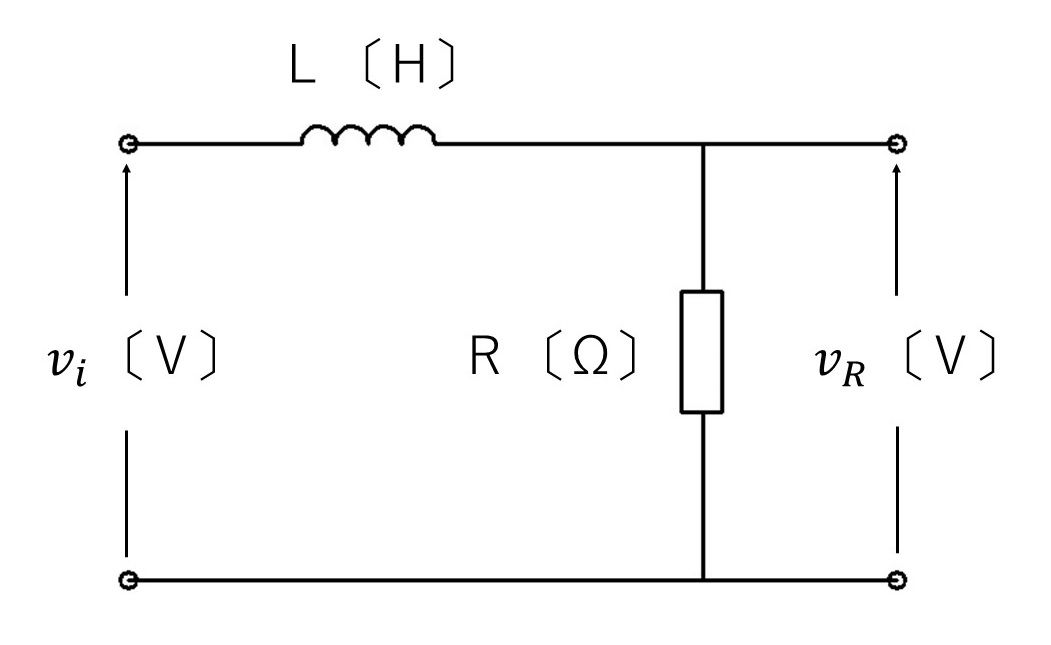
図1のようなインダクタンス $L$ 〔H〕のコイルと $R$ 〔Ω〕の抵抗からなる直列回路に、
図2のような振幅 $E$ 〔V〕、パルス幅 $T_0$ 〔s〕の方形波電圧 $v_i$ 〔V〕を加えた。
このときの抵抗 $R$ 〔Ω〕の端子間電圧 $v_R$ 〔V〕の波形を示す図として、正しいのはどれか?
ただし、図1の回路の時定数 $\cfrac{L}{R}$ 〔s〕は $T_0$ 〔s〕より十分小さく( $\cfrac{L}{R}\ \ll\ T_0$ )、
方形波電圧 $v_i$ 〔V〕を発生する電源の内部インピーダンスは0〔Ω〕とし、
コイルに流れる初期電流は0〔A〕とする。
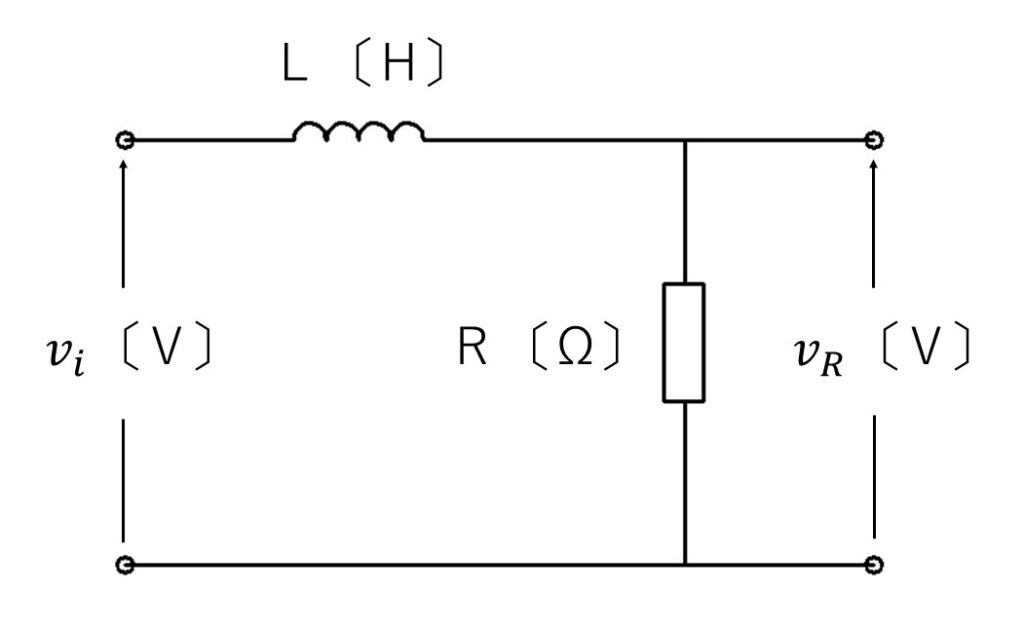
図1
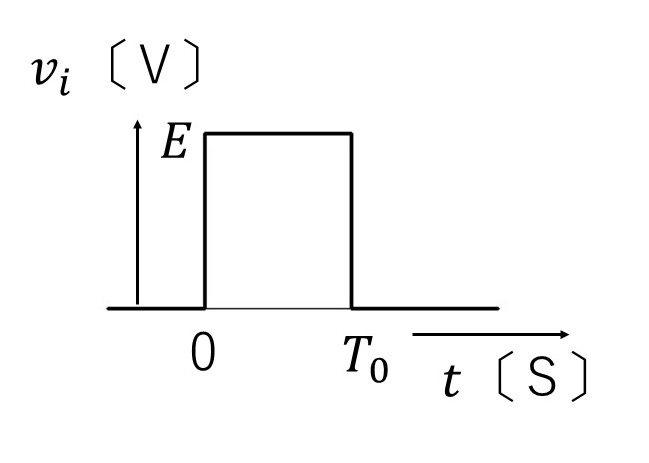
図2
(1)
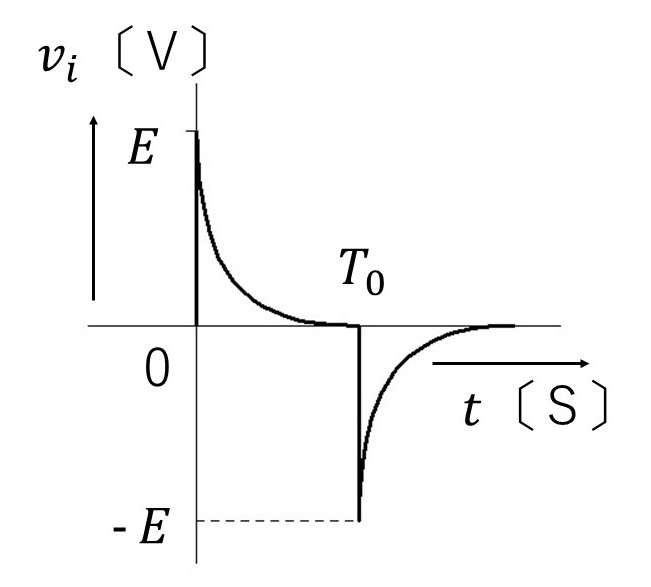
(2)
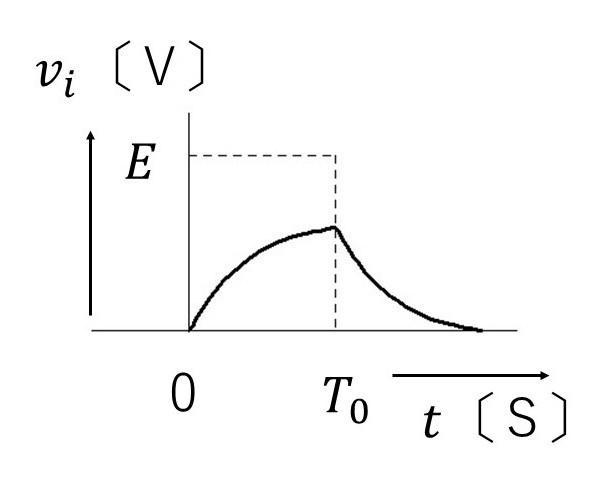
(3)
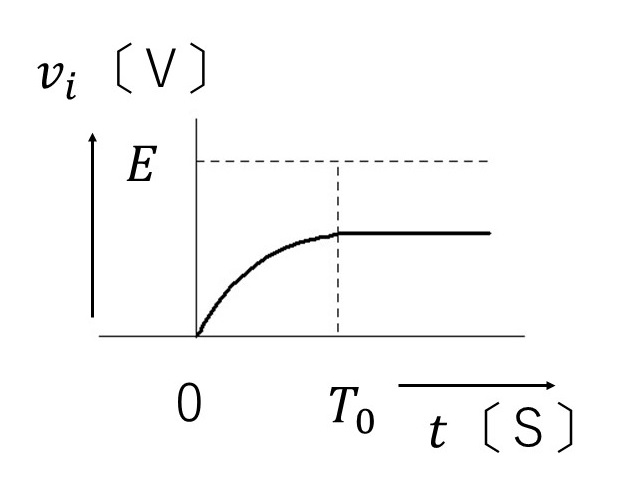
(4)
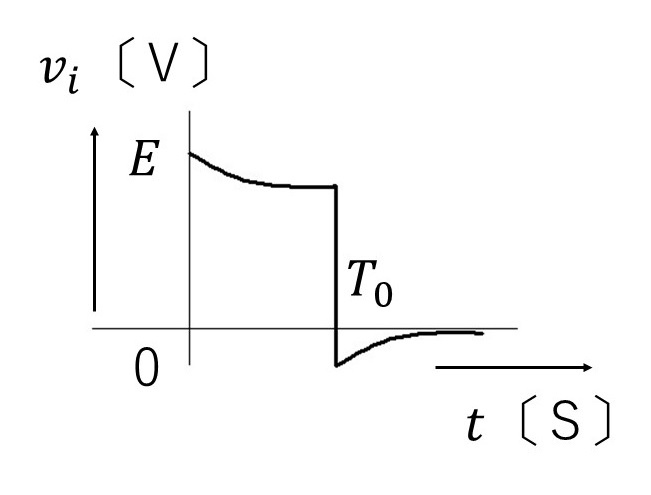
(5)
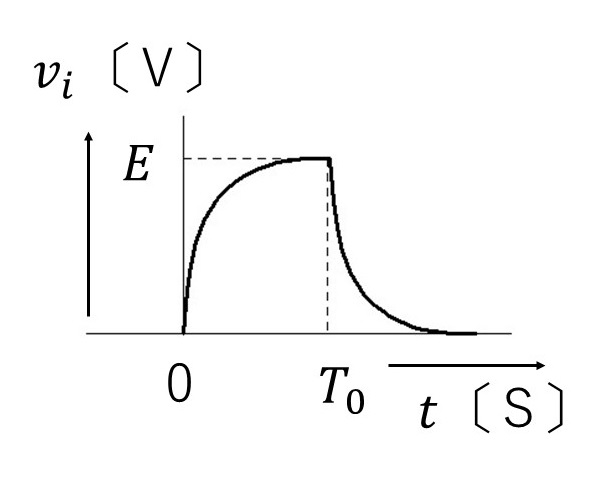
解答
正解は(5)
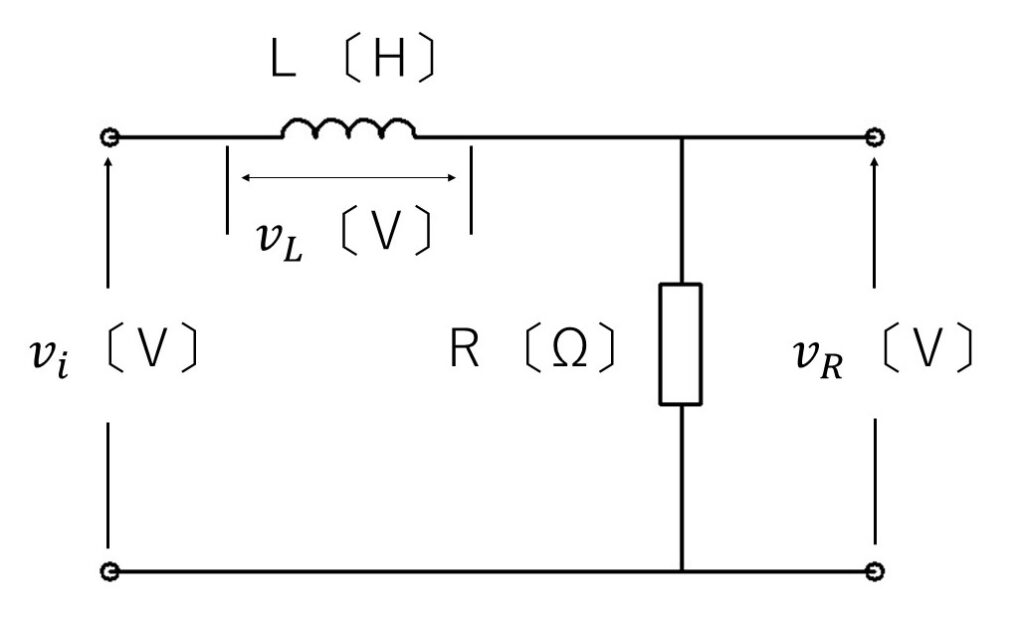
入力電圧 $v_i$ は、$v_L$ と $v_R$ を足したものです。
まず、コイルの両端の電圧 $v_L$ から見ていきましょう。
コイルのアマノジャクな性質により、直流電流を流そうとする(電圧が掛ける)と、それを阻止する方向に誘導起電力が発生します。
また、直流電流を止めようとする(電圧を0にする)と、流し続ける方向に誘導起電力が発生します。

これは、$v_L$ を表しています。
よって、コイルに方形波電圧の立ち上がり部分の電圧Eを加えた瞬間、コイルには誘導起電力(逆起電力)が発生し、電流が流れません。
コイルに電流が流れないということは、入力電圧 $v_i$ は全てコイルで消費されます。
$T=0$ 〔s〕において、コイルの両端の電圧 $v_L$ は、入力電圧 $v_i$ と等しいということです。
時間と共に、コイルに電流が流れるようになります。
最終的には、抵抗分が無くなり、普通の電線のごとく電流を流します。
また、$T_0$ において電圧が無くなった瞬間のコイルは電流を流し続けます。
流し続ける方向に、誘導起電力が働いているためです。
時間と共に電流は無くなり、最終的には電流はゼロになります。
これがコイルの直流電圧に対する動きです。
コイルの両端に掛かる電圧の動きは、上の解答群の(1)のグラフになります。
次に、抵抗の両端に掛かる電圧を考えましょう。
最初に書きましたが、$v_i=v_L+v_R$ の式が成り立ちます。
$v_R$ について式を書き換えると、$v_R=v_i-v_L$ です。
時間 $t$ が $0<t<T_0$ の間は $v_i=E$ なので、$v_R=E-v_L$ と書けます。
すると、$0<t<T_0$ の間の $v_R$ は解答群(5)の $0<t<T_0$ の間 $v_R$ なります。
時間 $t$ が $T_0<t$ の領域では $v_i=0$ なので、$v_R=0-v_L$ と書けます。
また、$t=T_0$ においてコイルに電流が流れ続けるとは、
回路に電流が流れ続けることであり、
抵抗に電流が流れ続けることです。
これは、$t=T_0$ において抵抗の電圧が $E$ から始まるということです。
解説
解答に、ダラダラと解説風を書いてしまったので、今回の解説は少し細かいところを。
まず、時定数についてです。
記号は $\tau$ です。(読みは「タウ」です。)
変化の割合が、63.2%になるまでの時間のことです。
今回の問題の正解(5)のグラフで説明すると、
立ち上がり部分の電圧が、$0.632E$ になった時の $t$ の値です。
また、立ち下がり部分においては、$0.368E$ になった時の $t$ の値です。
時定数の変化の割合が、なぜ63.2%なのか?
これは、マルっと覚えてください。
元式は、$\tau=1-\cfrac{1}{e}$
ここで、$e$ は自然対数の低(ネイピア数)のことです。
$e=2.71828$ (フナ、一鉢二鉢)なので、代入して、
$\tau=1-\cfrac{1}{2.71828}=0.63212\doteqdot0.632$ となります。
では、なぜ $\tau=1-\cfrac{1}{e}$ なのか?
過渡現象を極めてください。そこに出てきます。
次に、まったく意味のない説明ですが、
「図1の回路の時定数 $\cfrac{L}{R}$ 〔s〕は $T_0$ 〔s〕より十分小さく」の「十分小さく」についてですが、
今回の場合は「抵抗の電圧 $v_R$ が $E$ に達しているのですよ」を表すために出てきています。
時定数で見ると、$5\tau$ で99.3%に達します。
私の感覚では、「十分小さく」は「十分の1以下」だと思っています。
私の感覚など、何の意味も無いのですが。
この問題では、コイルについて問われています。
コイルが出てくると、当然コンデンサもどこかで出てくるはずですよね。
だから、コンデンサの動きも見ておきましょう。
コンデンサと抵抗の直列回路に、直流電圧を掛けると、
コンデンサに電荷が溜まり始めます。
電圧を掛けた瞬間は、あたかも電流が流れているように振る舞います。
この時のコンデンサの両端の電圧は、$0$〔V〕です。
時間と共に充電が進み、十分充電されると電流は流れなくなります。
最終的なコンデンサの両端の電圧は、電源電圧 $E$〔V〕になります。
また、電圧を $0$ 〔V〕としたとき、放電が始まります。
放電開始直後のコンデンサの両端の電圧は $E$ 〔V〕で、最終的には $0$ 〔V〕になります。
これをグラフで表すと、解答欄の(5)のようになります。

コンデンサと抵抗の直列回路の、抵抗の両端に現れる電圧は、解答欄の(1)になります。
時間 $t$ が $0<t<T_0$ の間は $v_i=E$ なので、$v_R=E-v_C$ と書けます。
また、時間 $t$ が $T_0<t$ の領域では $v_i=0$ なので、$v_R=0-v_C$ と書けます。
すると、

になります。
まとめ
コイルに直流電圧がかかった瞬間は、電流は流れません。
コイルの両端の電圧は、電源電圧です。
コンデンサに直流電圧がかかった瞬間は、普通の導線と同じように、電流が流れます。
コンデンサの両端の電圧は、$0$ 〔V〕です。
最終的に(定常状態に達すれば)コイルは、普通の導線のように、電流を流します。
また、コンデンサは、開いたスイッチのように、電流を流しません。
導線のように電流が流れると、電圧降下は起きません。
電流が流れないと、電源電圧はそこで消費されてしまします。
直流電圧に対する、コイルとコンデンサの振る舞いは、よく覚えておきましょう。
コメント