電験３種理論問題　Ｈ２１年　問６

問題

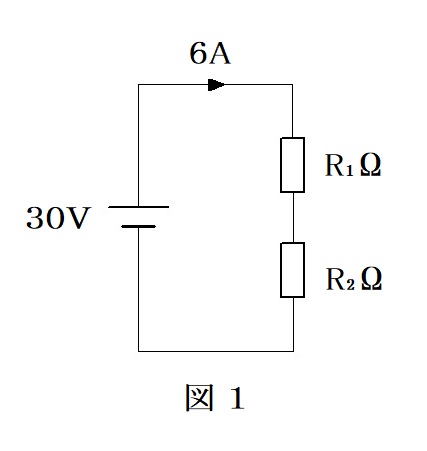
抵抗値の異なる抵抗 $R_1$ と $R_2$ を図１のように直列に接続し、３０〔Ｖ〕の直流電圧を加えたところ、回路に流れる電流は６〔Ａ〕であった。

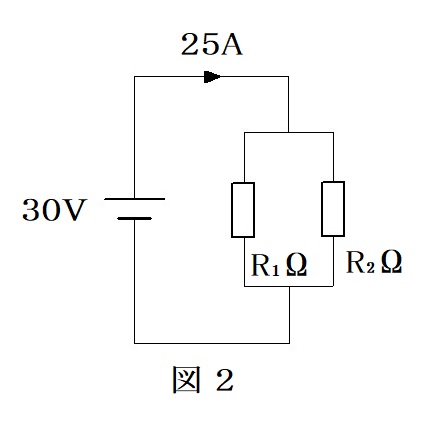
次に、この抵抗 $R_1$ と $R_2$ を図２のように並列に接続し、３０〔Ｖ〕の直流電圧を加えたところ、回路に流れる電流は２５〔Ａ〕であった。

このとき、抵抗 $R_1$ 、$R_2$ のうち小さい方の抵抗〔Ω〕の値として正しいのはどれか？

（１）　１　　（２）　１．２　　（３）　１．５　　（４）　２　　（５）　３

この問で必要な公式

公式①　$I=\frac{V}{R}$　〔A〕（オームの法則）

公式②　抵抗の直列接続　$R=R_1+R_2$

　　　　抵抗の並列接続　$R=\frac{R_1\times R_2}{R_1+R_2}$

公式③　解の公式　$a{x}^2+bx+c=0$　のとき

　$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$

解答

正解は、（４）

図１より、公式①　$I=\frac{V}{R}$　〔A〕を利用して

$6=\frac{30}{R_1+R_2}$ 　・・・・①

図２より、公式①　$I=\frac{V}{R}$　〔A〕を利用して

$25=\frac{30}{\frac{R_1\times R_2}{R_1+R_2}}$　・・・・②

①式より　$(R_1+R_2)\times 6=30$

　　　　　$R_1+R_2=\frac{30}{6}=5$　・・・・③

②式より　$25=\frac{30\times (R_1+R_2)}{R_1\times R_2}$　・・・・④

④式に③式を代入して

　　　　　$25=\frac{30\times 5}{R_1\times R_2}$

　　　　　$25\times (R_1\times R_2)=150$

　　　　　$R_1\times R_2=\frac{150}{25}=6$　・・・・⑤

③式より　$R_2=5-R_1$　・・・・⑥

⑤式に⑥式を代入して

　　　　　$R_1\times (5-R_1)=6$

　　　　　$-R_1^2+5R_1-6=0$

解の公式を利用して

$x=\frac{-5\pm \sqrt{5^2-4\times (-1)\times (-6)}}{2\times (-1)}$

$x=\frac{-5\pm \sqrt{25-24}}{-2}=\frac{5\pm 1}{2}$

$x=3or2$

$R_1=2$ ならば $R_2=3$ となり、$R_1=3$ ならば $R_2=2$ となります。

よって、小さい方の抵抗は、２Ω　となります。

解説

公式①は、オームの法則です。

（「電流は、電圧に比例し、抵抗に反比例する」と、私は文章で覚えています。）

公式②は、抵抗の直列・並列接続の合成抵抗の式です。

以上は、電験を受験するならば、当然覚えているべき公式です。

説明を省略します。と、言いたいのですが、それでは身も蓋もないので。

公式②の抵抗について、少し書いておきます。

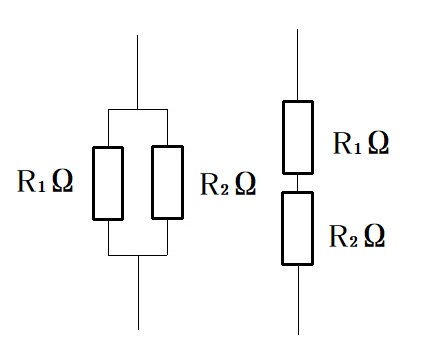
抵抗は、$R=\rho \frac{l}{S}$ と表すことができます。

$\rho$ は抵抗率で、単位は〔Ω・ｍ〕です。

$l$ は抵抗の長さで単位は〔m〕、$S$ は抵抗体の面積で単位は〔m²〕です。

並列接続では、面積が足されることになります。

上の図から、そのようにイメージしてください。

式で表すと、

$\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}$

$=\frac{S_1}{\rho l}+\frac{S_2}{\rho l}=\frac{S_1+S_2}{\rho l}$

となります。

抵抗が２つの並列接続の場合は、$R=\frac{R_1\times R_2}{R_1+R_2}$ で計算できます。

抵抗が３つ以上の並列接続の場合は、$\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}$ で計算しましょう。

抵抗の直列接続の場合は、長さが足されることになります。

これも、上の図からそのようにイメージしてください。

式で表すと、

$R=R_1+R_2$

$=\rho \frac{l_1}{S}+\rho \frac{l_2}{S}=\rho \frac{l_1+l_2}{S}$

となります。

何となく、簡単なものを複雑に説明している気がしますが、

$R=\rho \frac{l}{S}$ は、どこかで覚えないといけない公式ですから、ご勘弁を。

また、高校の時に習った「解の公式」ですが、たまに出てくるので確認しておいてください。

今回の場合は、$-R_1^2+5R_1-6=0$ に $-1$ を掛けて、

$R_1^2-5R_1+6=0$ として、因数分解すれば、

$(R_1-3)(R_1-2)=0$ となります。

実際の試験の時は、因数分解が早いと思えば因数分解で、

因数分解を思い付かないときは、「解の公式」で解いてください。

まとめ

この問題は、サービス問題ですね。

計算間違いで、せっかくのサービス問題を落とさないようにしましょう。