問題
図のように、点Oを中心とするそれぞれ半径1〔m〕と半径2〔m〕の円形導線の $\cfrac{1}{4}$ と、それらを連結する直線状の導線からなる扇形導線がある。この導線に、図に示す向きに直流電流 $I=8$ 〔A〕を流した場合、点Oにおける磁界〔A/m〕の大きさとして、正しいのは次のうちどれか。
ただし、扇形導線は同一平面上にあり、その巻数は一巻きである。
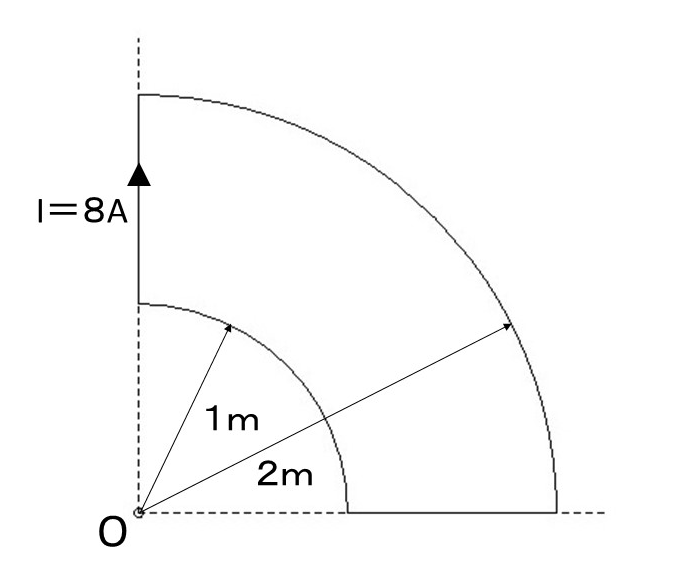
(1) 0.25 (2) 0.5 (3) 0.75 (4) 1.0 (5) 2.0
この問で必要な公式
① $H=\cfrac{I}{2\ r}$ 〔A/m〕
$H$ :磁界の強さ 〔A/m〕 $I$ :電流 〔A〕 $r$ :半径 〔m〕
解答
正解は(2)です。
この公式① $H=\cfrac{I}{2\ r}$ 〔A/m〕は、円周導体に $I$ 〔A〕の電流が流れた時、その円周の中心点における磁界の強さの公式です。
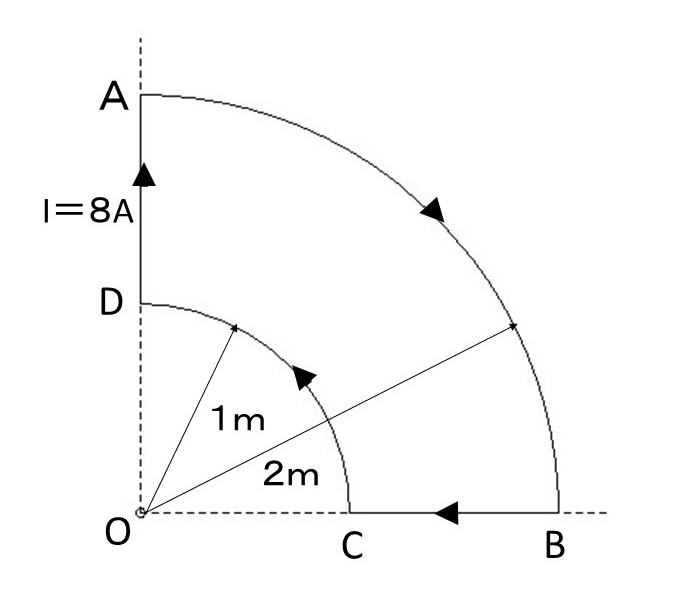
上図において、点A~B間の導体に電流8〔A〕が流れた時、点Oは
$H=\cfrac{1}{4}\times\cfrac{8}{2\times2}=0.5$ 〔A/m〕
の磁界の強さとなります。
向きは、右ねじの法則又は右手の法則により、紙面の裏側から表側に向かっています。
次に、点C~D間の導体に電流8〔A〕が流れた時、点Oは
$H=\cfrac{1}{4}\times\cfrac{8}{1\times2}=1$ 〔A/m〕
の磁界の強さとなります。
向きは、右ねじの法則又は右手の法則により、紙面の表側から裏側に向かっています。
これは、点A~B間の反対向きです。
よって、点Oの磁界の強さは
$H=1-0.5=0.5$ 〔A/m〕 となります。
向きは、紙面の表側から裏側に向かっています。
ちなみに、B~C間及びD~A間の導体による磁界の強さの影響は受けません。
解説
公式① $H=\cfrac{I}{2\ r}$ 〔A/m〕 と式の構成自体は簡単なので、そのまま覚えるのも一つの手です。
この式の元をたどっていけば、式がだんだん複雑になっていきます。
心して取り組んでください。
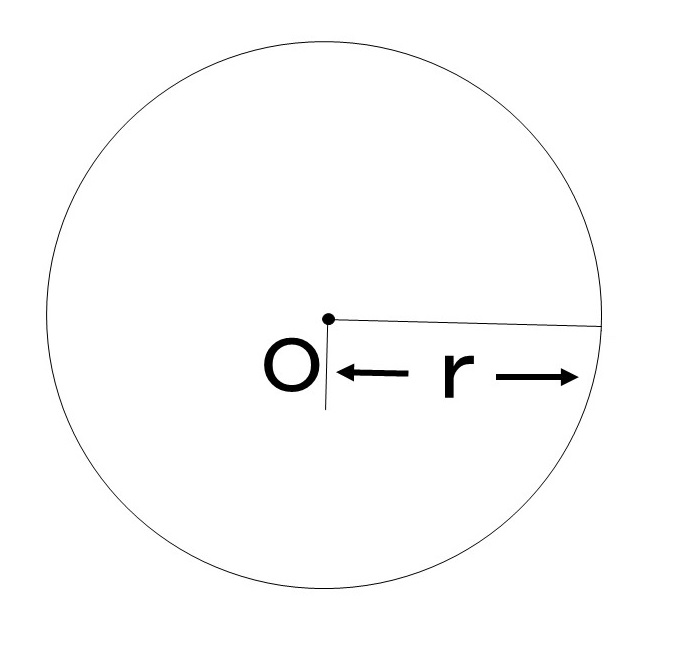
半径 $r$ の円形の導体に囲まれた、その円の中心の「磁界の強さ」が
公式① $H=\cfrac{I}{2\ r}$ 〔A/m〕 でした。
次に、
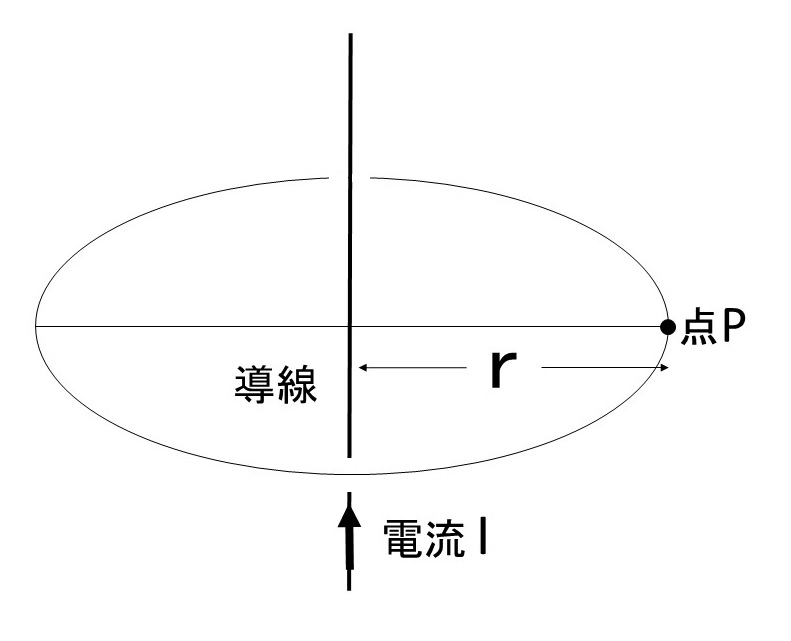
無限に長い直線導体から距離 $r$ 離れた点Pの「磁界の強さ」は
$H=\cfrac{I}{2\ \pi\ r}$ 〔A/m〕
この式を変形して、$2\ \pi\ r\ H=I$ となります。
これを言い換えると、「 $H$ の磁界の強さを円周の長さ分 $2\ \pi\ r$ 掛けると、電流 $I$ と等しくなる。」ということです。
これには法則名があり、「アンペアの周回積分の法則」と呼ばれています。
ここでは円を扱っているので「周回積分とは、円周の長さ分 $2\ \pi\ r$ 掛ける」ということです。
ここで私の私見ですが、
アンペアさんが $H$ を決めるとき、電流の〔アンペア〕を既に決めていたので、
「では、$H$ を周回積分すれば $I$ になると決めましょう」てなことになったのでは?
と思っています。
この無限に長い直線導体を $2\ \pi\ r$ 分だけ取り出し、それを円形に折り曲げれば、

この形になります。
$H=\cfrac{I}{2\ \pi\ r}$ 〔A/m〕から、$H=\cfrac{I}{2\ r}$ 〔A/m〕となり、 $\pi$ が取れます。
これを数学的に説明することは、私にはできませんが、
「まーるく、すれば、$\pi$ が取れる。」と言うことはできます。
公式① $H=\cfrac{I}{2\ r}$ 〔A/m〕を、ちゃんと数学的に説明しようとすると、
一気に面倒になります。
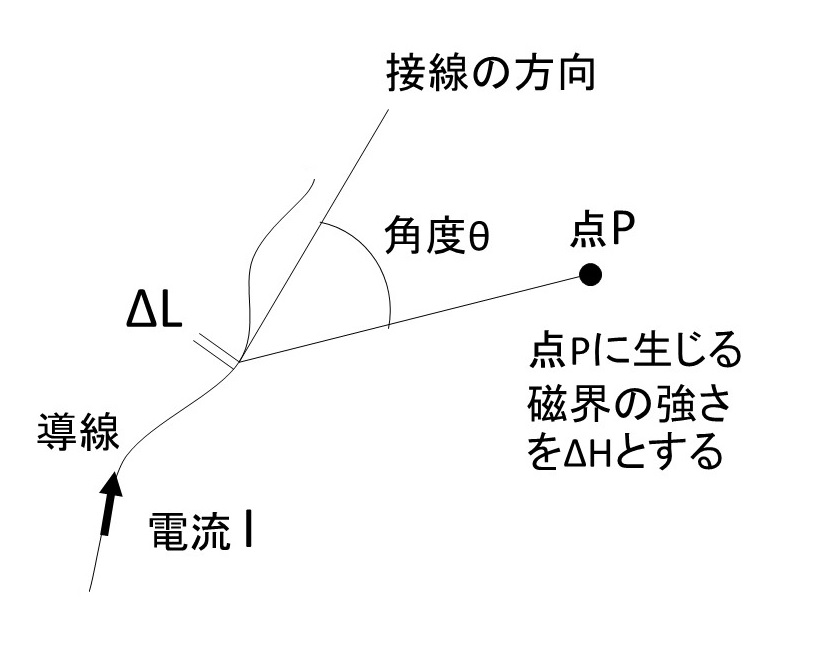
電流 $I$ の流れている導線の任意の微小部分 ΔL が点 P に作る磁界の強さ H は
(ΔL~点P間の長さをrとして)
$\varDelta\ H=\cfrac{I\ \sin\theta\ \varDelta\ L}{4\ \pi\ r^2}$ となります。
分母の $4\ \pi\ r^2$ は球の表面積です。
電流 $I$ の流れる電線の任意の(点に近い)微小部分 $\varDelta\ L$ が、点Pに与える微小な磁界の強さ $\varDelta\ H$ は、あくまで電線に発生する磁界なので、電線の横方向に発生します。
そして、接線の方向には発生しません。
$\angle90$ では、1になり。$\angle0$ では、0になります。
その間の角度では、$\sin\theta$ に比例します。
この問題のB~C間及びD~A間の導体による磁界の強さの影響を受けないのはこのためです。
(これを、ビオサバールの法則と言います。)
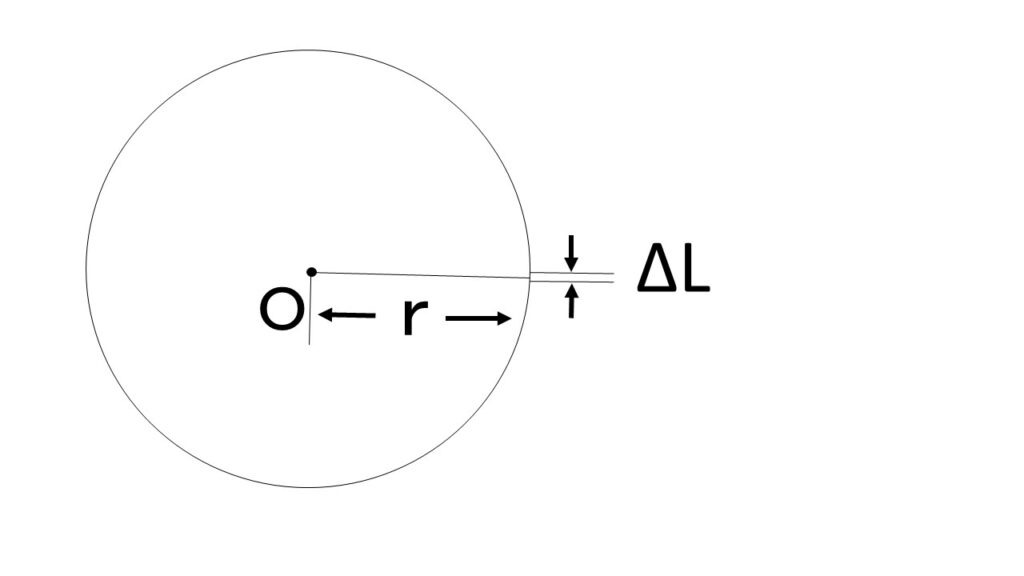
ビオサバールの法則を、円周導体の磁界の強さに当てはめてみましょう。
導体上の任意の箇所の微小部分 $\varDelta\ L$ の接線の方向と中心Oとは、常に直角です。
ということは、$\varDelta\ H=\cfrac{I\ \sin\theta\ \varDelta\ L}{4\ \pi\ r^2}$ の $\sin\theta$ は $\sin\theta=\sin\angle90=1$ なので、省略できます。
すると、$\varDelta\ H=\cfrac{I\ \varDelta\ L}{4\ \pi\ r^2}$ となります。
ここで、「 $\varDelta\ L$ 」を周回積分すると「 $2\ \pi\ r$ 」となります。
上の式に代入して、$H=\cfrac{I\ (2\ \pi\ r)}{4\ \pi\ r^2}$ となります。
これを整理して、公式①$H=\cfrac{I}{2\ r}$ 〔A/m〕となります。
「ビオサバールの法則」のくだりは面倒なので、今は覚えなくても良いと思います。
無限直線導体から $r$ 離れた点の磁界 $H=\cfrac{I}{2\ \pi\ r}$ 〔A/m〕と
円形導体の中心の磁界 $H=\cfrac{I}{2\ r}$ 〔A/m〕は覚えておきましょう。
まとめ
この公式① $H=\cfrac{I}{2\ r}$ 〔A/m〕は、色々と省略されているため、覚え易くもあり、忘れ易くもあり、ですね。
かと言って、「ビオサバールの法則」まで遡って導出方法を覚えるのも面倒ですよね。
だから、無限直線導体の磁界 $H=\cfrac{I}{2\ \pi\ r}$ 〔A/m〕と
円形導体の磁界 $H=\cfrac{I}{2\ r}$ 〔A/m〕を
セットで覚えるのはどうでしょうと提案しました。
ただ、無限直線導体の磁界 $H=\cfrac{I}{2\ \pi\ r}$ 〔A/m〕の説明も弱いですよね。
何か良い方法があれば、私に教えてください。
オマケ
遠藤のへそ毛はアイパー直毛。
遠藤(円形導体)の、へそ毛(中心点Pがへそで、毛がHを表す)はアイパー(アイロンパーマのこと・$I$/)直毛(直径= $2\ r$ )。
これも苦しい。
コメント