問題
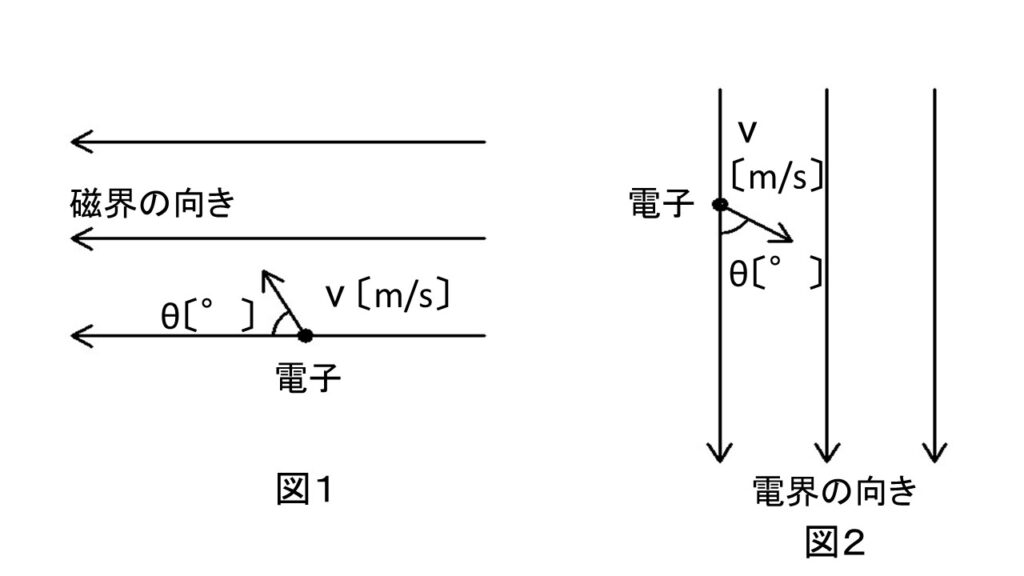
図1のように、真空中において強さが一定で一様な磁界中に、速さ $v$ 〔m/s〕の電子が磁界の向きに対して $\theta$ 〔°〕の角度( $0^\circ<\theta<90^\circ$ )で突入した。
この場合、電子は進行方向にも磁界の向きにも ( ア ) 方向の電磁力を常に受けて、その軌道は、 ( イ ) を描く。
次に、電界中に電子を置くと、電子は電界の向きと ( ウ ) 方向の静電力を受ける。
また、図2のように、強さが一定で一様な電界中に、速さ $v$ 〔m/s〕の電子が電界の向きに対して $\theta$ 〔°〕の角度( $0^\circ<\theta<90^\circ$ )で突入したとき、その軌跡は、 ( エ ) を描く。
上記の記述中の(ア)(イ)(ウ)(エ)に当てはまる語句として、正しいものの組み合わせはどれか?
(1)(ア)反対 (イ)らせん (ウ)反対 (エ)放物線
(2)(ア)直角 (イ)円 (ウ)同じ (エ)円
(3)(ア)同じ (イ)円 (ウ)直角 (エ)放物線
(4)(ア)反対 (イ)らせん (ウ)同じ (エ)円
(5)(ア)直角 (イ)らせん (ウ)反対 (エ)放物線
基礎知識
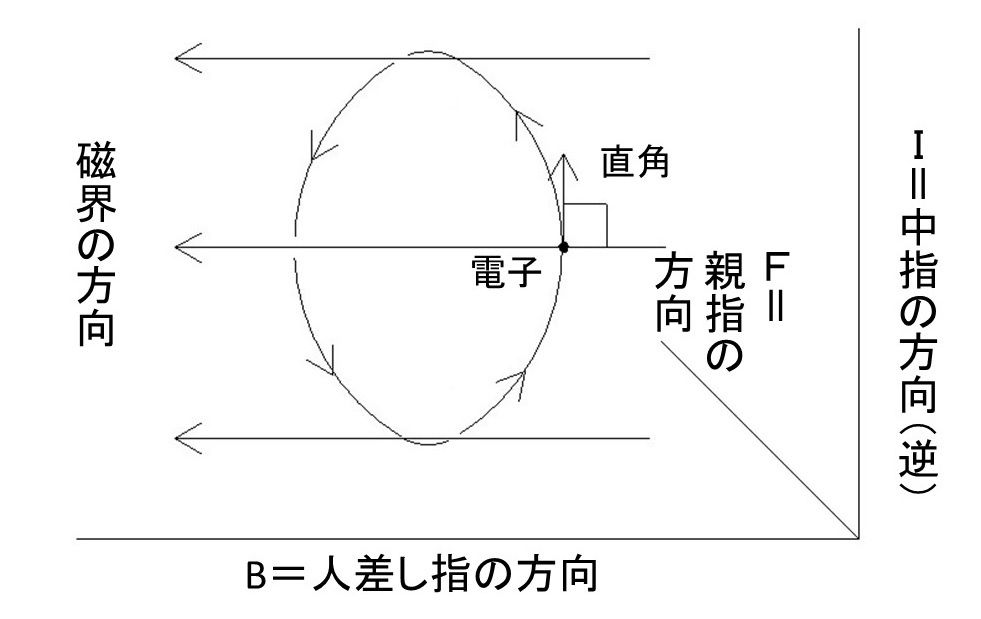
磁界中に帯電体が磁界と直角に進入した時、帯電体には磁界方向と進入方向の両方に直角の方向に力が働きます。
この図では、電子に働く力なので、電流の方向(+の帯電体の移動する方向)と逆になります。
この力を、ローレンツ力と言います。
式で表すと、$F=Bqv$ 〔N〕となります。
$F$ はローレンツ力〔N〕、$B$ は磁界の強さ〔T〕、$q$ は電気量(電荷)〔C〕、$v$ は帯電体の速度〔m/s〕になります。
その力の向きは、フレミングの左手の法則によります。
親指が力の方向、人差し指が磁界の向き、中指が(+)の電荷が動く向きになります。
(電子の動きなので、中指の向きが逆になります。注意してください)
フレミングの左手の法則は、一般的には、電磁力の向きを表す法則として出てきていますよね。
電磁力とは、磁界の中に垂直に電気の流れている電線を置いた時の、電線が受ける力です。
式は、$F=Bil$ 〔N〕です。
$F$ は電磁力〔N〕、$B$ は磁界の強さ〔T〕、$i$ は電流〔A〕、$l$ は電線の長さ〔m〕です。
帯電体や電線が、磁界に対して垂直ではなく角度をもっていれば、$sin\theta$ が掛かってきます。
これは、磁界の向きと平行に移動する帯電体や、磁界の向きと平行に置かれた電線には何の力も働かいということです。
次に、電界の話です。
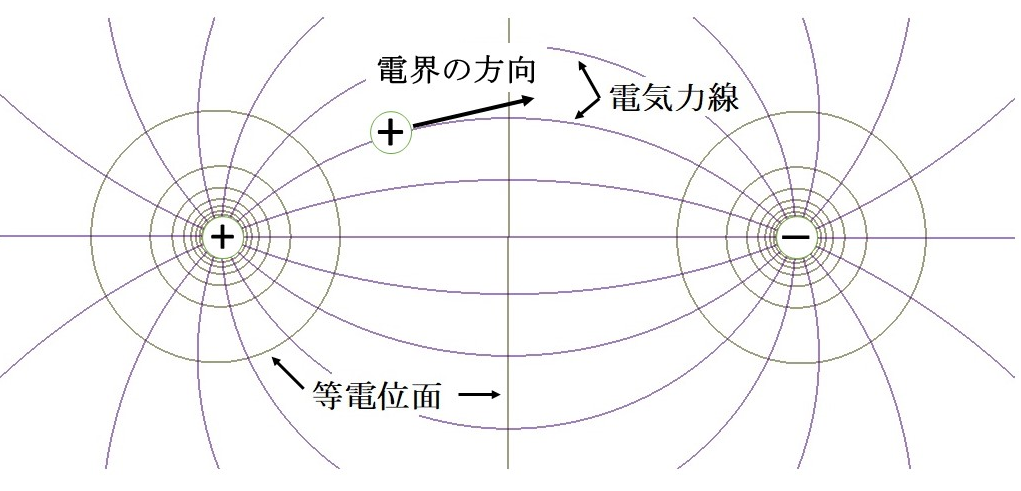
電界は、電気力線の存在する場です。
電気力線は、(+)から(-)に向かいます。
電界に置かれた(+)の電荷を持つ帯電体は、電界の方向に力を受けます。
この力を、静電力と言います。
式で表すと、$F=qE$ となります。
ここで、$F$ 〔N〕は帯電体が受ける力、$q$ 〔C〕は帯電体の電荷、$E$ 〔V/m〕は電界の強さ、を表します。
解答
正解は(5)です。
基礎知識の最初の図のように、電界に直角に電子が侵入すると、円運動をします。
この問では、角度 $\theta$ を持って進入すると、
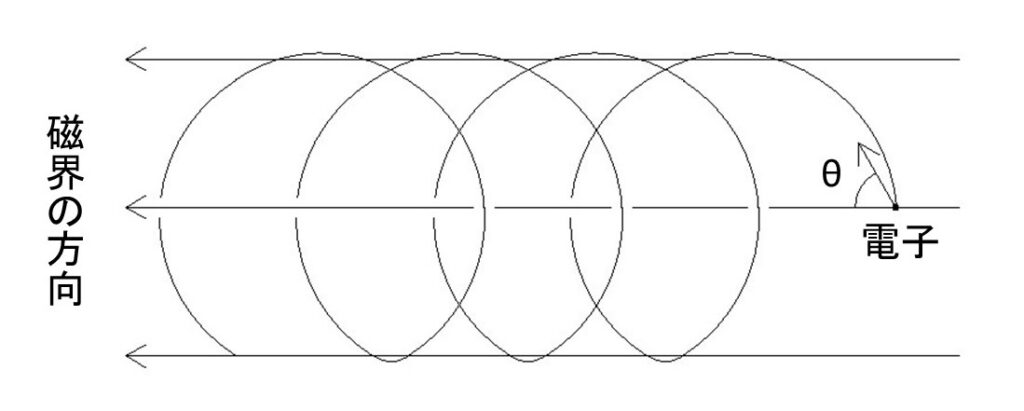
図のように、電子の速度ベクトルに対して $v\ cos\theta$ 分の等速運動をしつつ、
$v\ sin\theta$ 分の円運動をします。
この二つを合成すると、図のような「らせん運動」となります。
次に、電界中に電子が角度 $\theta$ で進入すると、
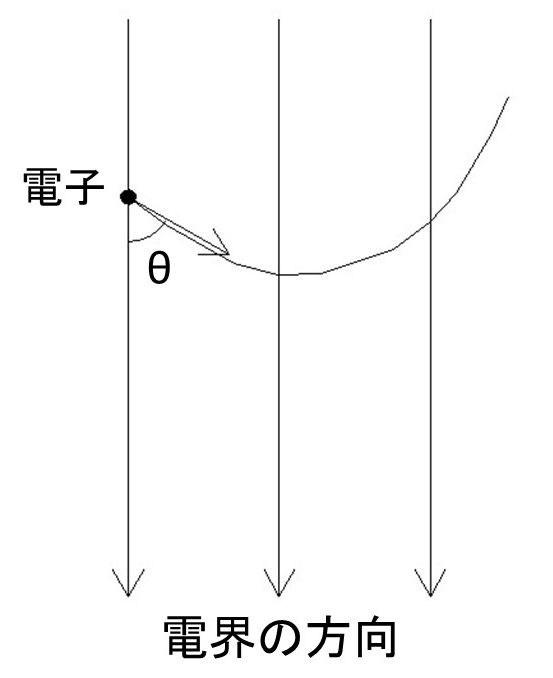
電界からの力 $F=Eq$ を受けることになります。
「+」の帯電体は電界の方向に力を受けますが、電子は「-」の帯電体なので電界の方向と逆方向に力を受けます。
よって、図のように放物線を描きます。
まとめ
電子は、「-」の帯電体なので電流の向きと逆になります。
フレミングの左手の法則の中指の向きが逆になります。(右手になってしまいます。)
電界の中での力の方向も逆になります。
気を付けてください。
ちなみに、私は、フレミングの法則(右手も左手も)について、親指が「F」、人差し指が「B」、中指が「I」と覚えています。
「F」が力の方向や電線の進む方向。
「B」が磁界の向き。
「I」が電流の向きや「+」の帯電体が進む方向。
です。
親指から「FBI」(アメリカの連邦捜査局)と覚えています。
磁界中の電子の動き、電界中の電子の動きの基礎的なイメージを理解するのに良い問題だと思います。
よく読んで、頭の中にイメージ図を入れておいてください。

コメント