問題
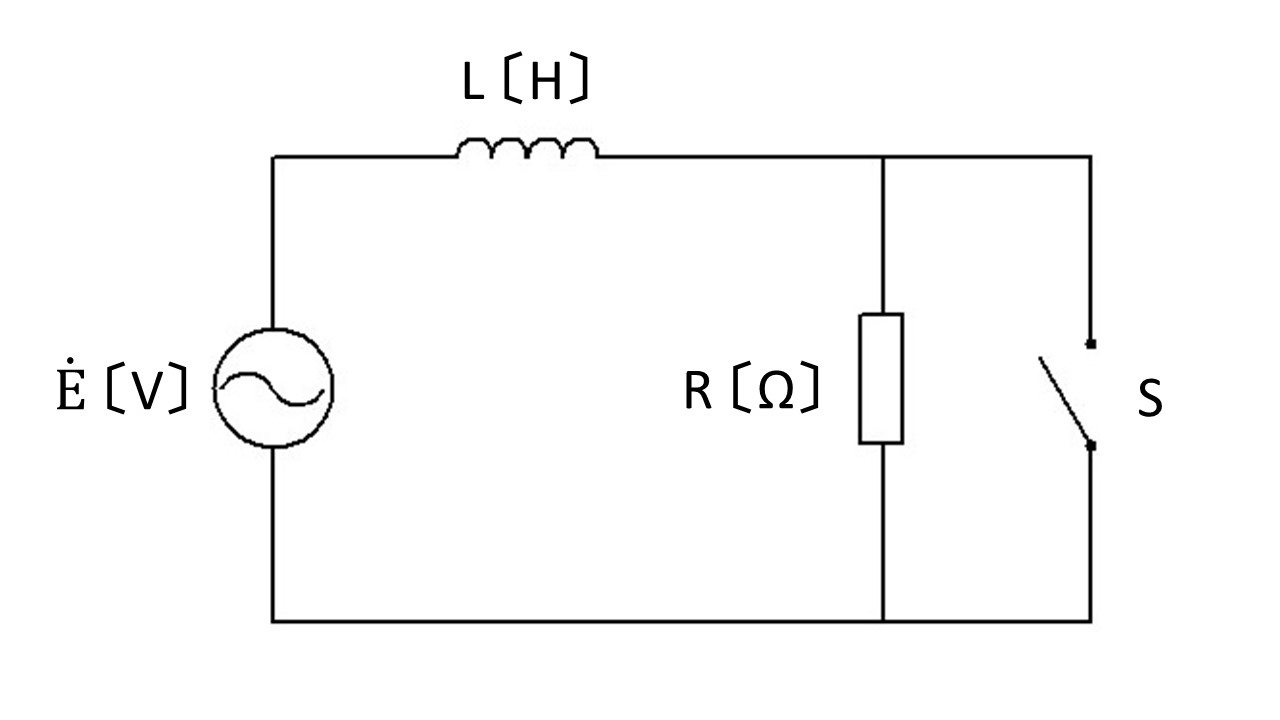
図のように、$R=\sqrt{3}\omega L$ 〔Ω〕の抵抗、インダクタンス $L$ 〔H〕のコイル、スイッチSが各周波数 $\omega$ 〔rad/s〕の交流電圧 $\dot{E}$ 〔V〕の電源に接続されている。
スイッチSを開いているとき、コイルを流れる電流の大きさを $I_1$ 〔A〕、電源電圧に対する電流の位相差を $\theta_1$ 〔°〕とする。
また、スイッチSを閉じているとき、コイルに流れる電流の大きさを $I_2$ 〔A〕、電源電圧に対する電流の位相差を $\theta_2$ 〔°〕とする。
このとき、$\cfrac{I_1}{I_2}$ 及び $|\theta_1-\theta_2|$ 〔°〕の値として正しいものの組み合わせはどれか?
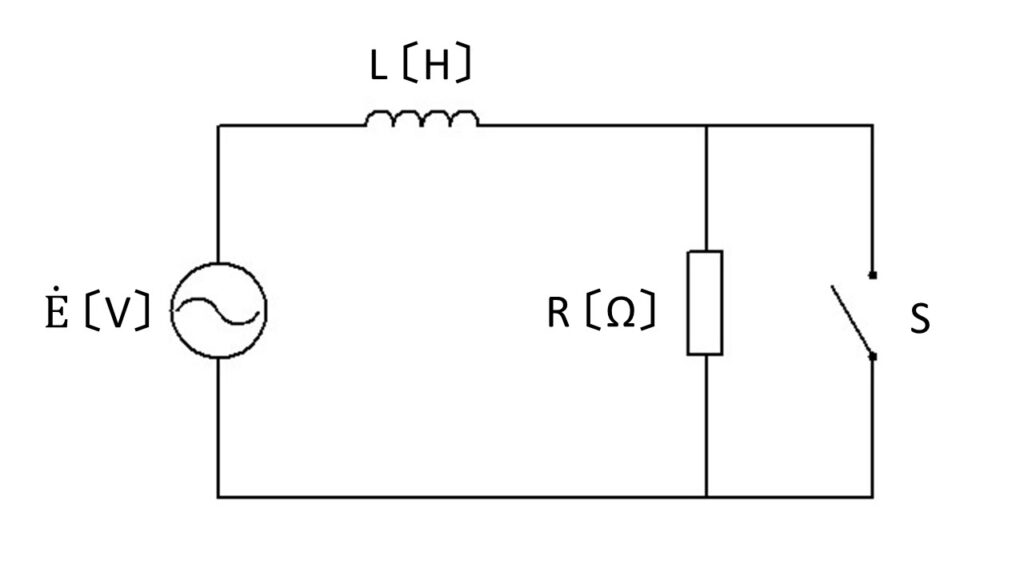
(1) $\cfrac{I_1}{I_2}=\cfrac{1}{2}$ $|\theta_1-\theta_2|=30$
(2) $\cfrac{I_1}{I_2}=\cfrac{1}{2}$ $|\theta_1-\theta_2|=60$
(3) $\cfrac{I_1}{I_2}=2$ $|\theta_1-\theta_2|=30$
(4) $\cfrac{I_1}{I_2}=2$ $|\theta_1-\theta_2|=60$
(5) $\cfrac{I_1}{I_2}=2$ $|\theta_1-\theta_2|=90$
この問で必要な公式
① $I=\cfrac{|\dot{E}|}{|\dot{Z}|}$
② $\dot{Z}=R+\Bigl(j\omega L-j\cfrac{1}{\omega C}\Bigr)$
解答
正解は(2)です。
スイッチSが「開」のときのインピーダンスZは?
公式②より、$\dot{Z}=R+j\omega L$ となります。
これを公式①に代入すると、
$\dot{I}_1=\cfrac{|\dot{E}|}{|\dot{Z}|}=\cfrac{|\dot{E}|}{R+j\omega L}$
$|\dot{E}|=E$ と表すこととし、また題意より、$R=\sqrt{3}\omega L$ なので、これを代入して、
$\dot{I}_1=\cfrac{E}{\sqrt{3}\omega L+j\omega L}$
分母を有理化して、
$\dot{I}_1=\cfrac{E(\sqrt{3}\omega L-j\omega L)}{(\sqrt{3}\omega L+j\omega L)(\sqrt{3}\omega L-j\omega L)}$
$=\cfrac{(E\omega L)(\sqrt{3}-j)}{3\omega^2 L^2+\omega^2 L^2}=\cfrac{(E\omega L)(\sqrt{3}-j)}{4\omega^2 L^2}$
$=\cfrac{E(\sqrt{3}-j)}{4\omega L}=\cfrac{\sqrt{3}E}{4\omega L}-\cfrac{jE}{4\omega L}$
$\dot{I}_1$ の大きさ $|\dot{I}_1|=I_1$ を求めます。
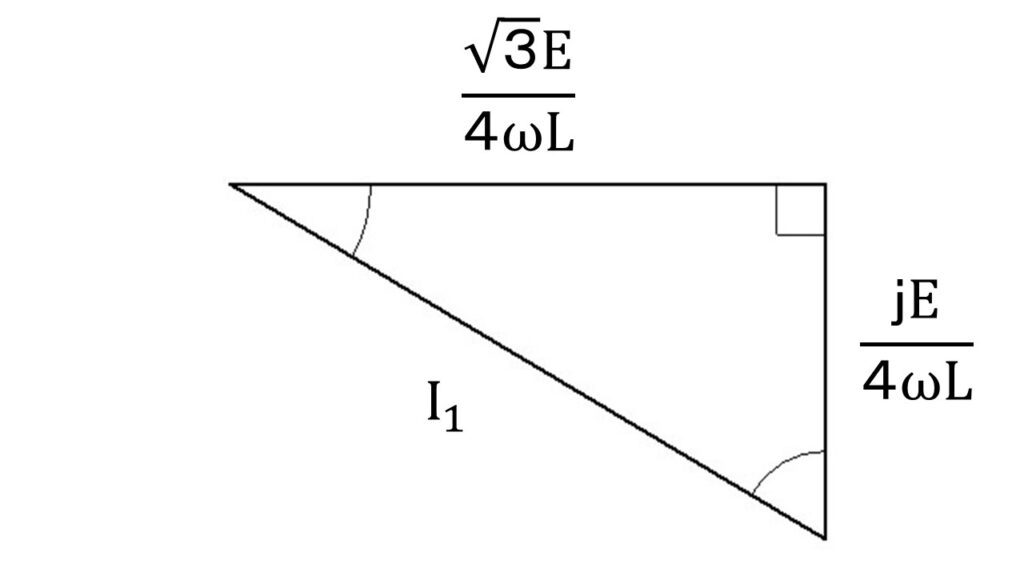
三平方の定理より、
$I_1=\sqrt{\left(\cfrac{\sqrt{3}E}{4\omega L}\right)^2+\left(\cfrac{E}{4\omega L}\right)^2}$
$=\sqrt{\cfrac{3E^2}{16\omega^2L^2}+\cfrac{E^2}{16\omega^2L^2}}=\sqrt{\cfrac{4E^2}{16\omega^2L^2}}$
$=\cfrac{2E}{4\omega L}=\cfrac{E}{2\omega L}$
となります。
$\theta_1$ を求めます。
$tan\theta_1=\cfrac{\mbox{虚数軸の値}}{\mbox{実数軸の値}}$ となりますよね。
数値を当てはめると、
$tan\theta_1=\cfrac{\cfrac{E}{4\omega L}}{\cfrac{\sqrt{3}E}{4\omega L}}=\cfrac{1}{\sqrt{3}}$
となります。
角度を求めるのに、$tan^{-1}$ を取ると、
$tan^{-1}\cfrac{1}{\sqrt{3}}=30^\circ$
(数式上この様に書きましたが、計算をするのではなく、上の図を描いて値を求めてください。)
となります。
次にスイッチSが「閉」のとき、電流はR側を流れないで全てスイッチ側を流れます。
よって、スイッチSが「閉」のときのインピーダンスZは、
$Z=j\omega L$ です。
これを公式①に代入すると、
$I_2=\cfrac{E}{\omega L}$
となります。
$\theta_2$ は、負荷が $\omega L$ だけなので、90°(遅れ)です。
問の、
$\cfrac{I_1}{I_2}=\cfrac{\cfrac{E}{2\omega L}}{\cfrac{E}{\omega L}}$
$=\cfrac{\cfrac{1}{2}}{1}=\cfrac{1}{2}$
であり、
$|\theta_1-\theta_2|=|30-90|=60$
となります。
解説
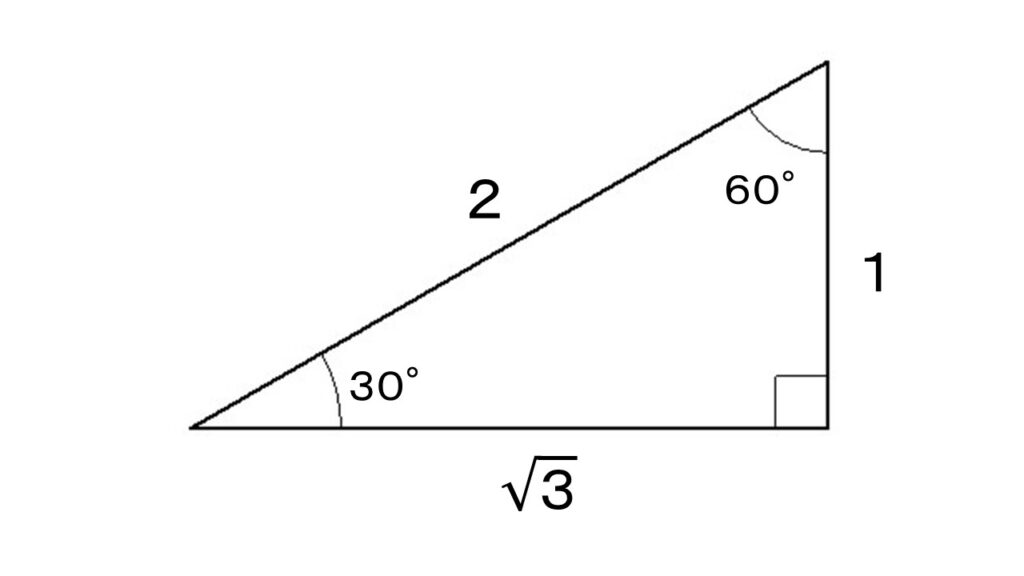
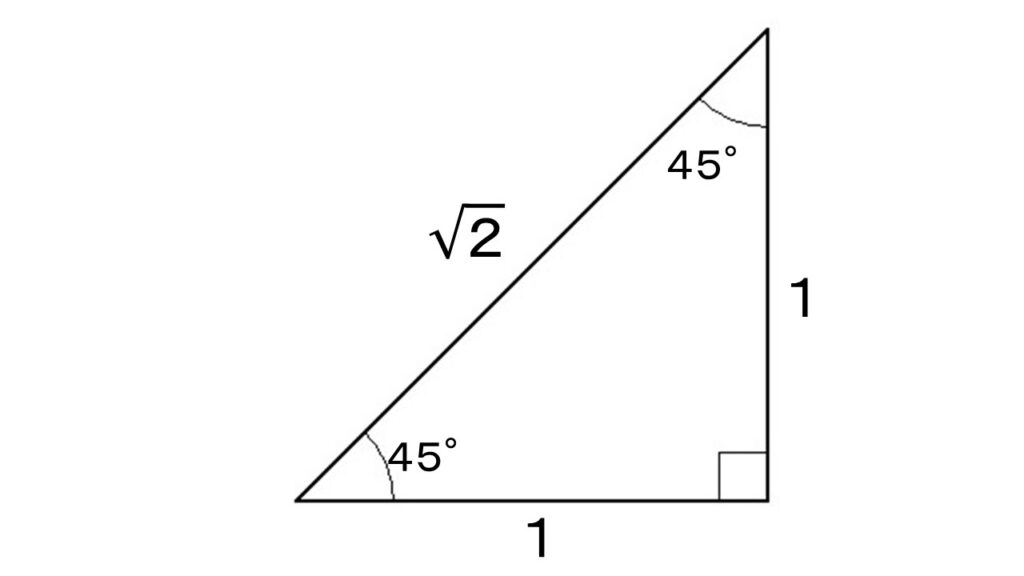
図から明らかなように、
$sin0^\circ=0$ 、 $sin30^\circ=\cfrac{1}{2}$
$sin45^\circ=\cfrac{1}{\sqrt{2}}$ 、 $sin60^\circ=\cfrac{\sqrt{3}}{2}$
$sin90^\circ=1$
$cos0^\circ=1$ 、 $cos30^\circ=\cfrac{\sqrt{3}}{2}$
$cos45^\circ=\cfrac{1}{\sqrt{2}}$ 、 $cos60^\circ=\cfrac{1}{2}$
$cos90^\circ=0$
$tan30^\circ=\cfrac{1}{\sqrt{3}}$ 、 $tan45^\circ=1$
$tan60^\circ=\sqrt{3}$
となります。
以上の $sin$ 、$cos$ 、$tan$ はよく覚えておきましょう。
関数電卓が使えない今は、これくらいしか出てきません。
また、公式① $I=\cfrac{|\dot{E}|}{|\dot{Z}|}$ の $|\dot{Z}|$ はインピーダンスZの大きさです。
三平方の定理 $a^2+b^2=c^2$ を使っています。
だから、公式② $\dot{Z}=R+\Bigl(j\omega L-j\cfrac{1}{\omega C}\Bigr)$ で求めたリアクタンスXの虚数表示 $j$ をあえて取っています。
虚数表示 $j$ があると、$a^2-b^2\neq c^2$ となり、定理に合いません。
間違える人も少ないと思いますが、一言。
また、スイッチSを「閉」とすると抵抗に電流が流れません。
電流は流れ易い方に流れるので、抵抗のないスイッチSに全て流れます。
抵抗Rは、無視して考えてください。
まとめ
30°、60°、90°の三角形の辺の比と、45°、45°、90°の三角形の辺の比は、覚えておきましょう。
「 $1:2:\sqrt{3}$ 」と「 $1:1:\sqrt{2}$ 」を穴の空くほど眺めましょう。
また、声に出して、呪文のように唱えてみましょう。
複素数の計算にも、慣れておいてください。
分母に虚数が含まれている場合は、分母の複素数の共役複素数を分母分子に掛けます。
(共役複素数とは、元の複素数の「 $j$ 」の前の符号を変えた複素数です。)
$a\pm jb$ が元の複素数ならば、$a\mp jb$ が共役複素数です。
これらを掛け合わせると、
$(a\pm jb)(a\mp jb)=a^2+b^2$ となり、分母の虚数 $j$ が消えます。
分母の虚数 $j$ が消えると、複素数を実数部と虚数部に分けることができますよね。
この問題の場合は、実数部が抵抗を流れる電流、虚数部がコイルを流れる電流となります。
コメント