問題
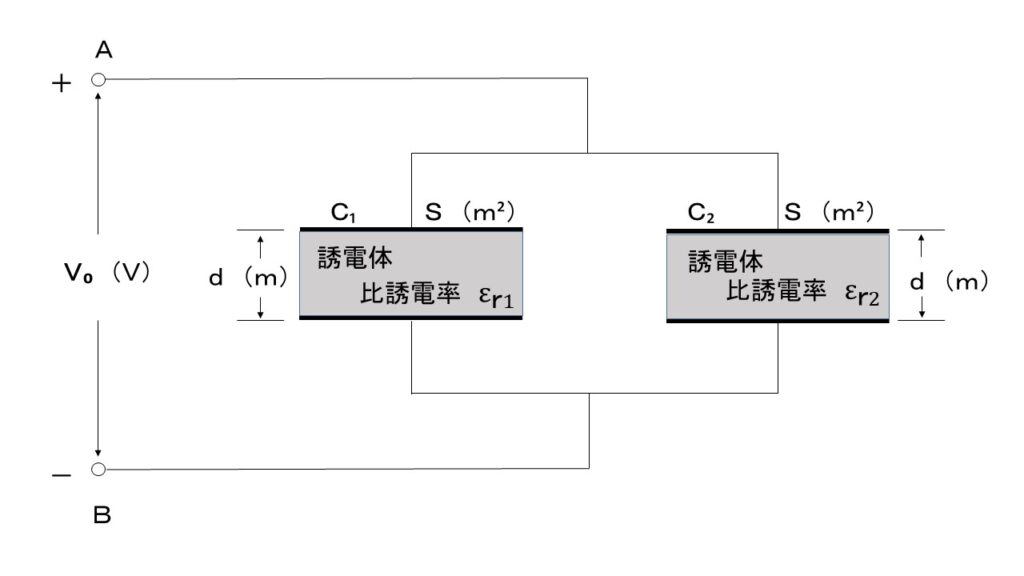
電極板面積と電極板間隔が共にS〔$m^2$〕とd〔m〕で、一方は比誘電率が $\varepsilon_{r1}$ の誘電体からなる平行平板コンデンサC₁と、他方は比誘電率 $\varepsilon_{r2}$ の誘電体からなる平行平板コンデンサC₂ がある。
いまこれらを図のように並列に接続し、端子A、B間に直流電圧V₀〔V〕を加えた。
このとき、コンデンサC₁の電極板間の電界の強さをE₁〔V/m〕、電束密度をD₁〔$C/m^2$〕。
また、コンデンサC₂ の電極板間の電界の強さをE₂〔V/m〕、電束密度をD₂〔$C/m^2$〕とする。
両コンデンサの電界の強さE₁〔V/m〕とE₂〔V/m〕はそれぞれ ( ア ) であり、
電束密度 D₁〔$C/m^2$〕とD₂〔$C/m^2$〕はそれぞれ ( イ ) である。
したがって、コンデンサC₁ に蓄えられる電荷をQ₁〔C〕、コンデンサC₂ に蓄えられる電荷をQ₂〔C〕とすると、それらはそれぞれ ( ウ ) となる。
ただし、電極板の厚さ及びコンデンサの端効果は、無視できるものとする。また、真空中の誘電率を $\varepsilon_0$ 〔F/m〕とする。
1 ア $E_1=\cfrac{\varepsilon_{r1}}{d}V_0$ と $E_2=\cfrac{\varepsilon_{r2}}{d}V_0$
イ $D_1=\cfrac{\varepsilon_{r1}}{d}SV_0$ と $D_2=\cfrac{\varepsilon_{r2}}{d}SV_0$
ウ $Q_1=\cfrac{\varepsilon_0\varepsilon_{r1}}{d}SV_0$ と $Q_2=\cfrac{\varepsilon_0\varepsilon_{r2}}{d}SV_0$
2 ア $E_1=\cfrac{\varepsilon_{r1}}{d}V_0$ と $E_2=\cfrac{\varepsilon_{r2}}{d}V_0$
イ $D_1=\cfrac{\varepsilon_0\varepsilon_{r1}}{d}V_0$ と $D_2=\cfrac{\varepsilon_0\varepsilon_{r2}}{d}V_0$
ウ $Q_1=\cfrac{\varepsilon_0\varepsilon_{r1}}{d}SV_0$ と $Q_2=\cfrac{\varepsilon_0\varepsilon_{r2}}{d}SV_0$
3 ア $E_1=\cfrac{V_0}{d}$ と $E_2=\cfrac{V_0}{d}$
イ $D_1=\cfrac{\varepsilon_0\varepsilon_{r1}}{d}SV_0$ と $D_2=\cfrac{\varepsilon_0\varepsilon_{r2}}{d}SV_0$
ウ $Q_1=\cfrac{\varepsilon_0\varepsilon_{r1}}{d}V_0$ と $Q_2=\cfrac{\varepsilon_0\varepsilon_{r2}}{d}V_0$
4 ア $E_1=\cfrac{V_0}{d}$ と $E_2=\cfrac{V_0}{d}$
イ $D_1=\cfrac{\varepsilon_0\varepsilon_{r1}}{d}V_0$ と $D_2=\cfrac{\varepsilon_0\varepsilon_{r2}}{d}V_0$
ウ $Q_1=\cfrac{\varepsilon_0\varepsilon_{r1}}{d}SV_0$ と $Q_2=\cfrac{\varepsilon_0\varepsilon_{r2}}{d}SV_0$
5 ア $E_1=\cfrac{\varepsilon_0\varepsilon_{r1}}{d}SV_0$ と $E_2=\cfrac{\varepsilon_0\varepsilon_{r2}}{d}SV_0$
イ $D_1=\cfrac{\varepsilon_0\varepsilon_{r1}}{d}V_0$ と $D_2=\cfrac{\varepsilon_0\varepsilon_{r2}}{d}V_0$
ウ $Q_1=\cfrac{\varepsilon_{r1}}{d}SV_0$ と $Q_2=\cfrac{\varepsilon_{r2}}{d}SV_0$
この問で必要な公式
① $V=E\ d$ 〔V〕
② $D=\varepsilon\ E$ 〔$C/m^2$〕
③ $C=\varepsilon\:\cfrac{S}{d}$ 〔F〕
④ $Q=C\ V$ 〔C〕
E:電界の強さ(V/m) V:電圧(V) d:極板間隔(m)
D:電束密度(C/m²) S:面積(m²) C:静電容量(F)
Q:電荷(C) $\varepsilon=\varepsilon_r\varepsilon_0$:誘電率〔F/m〕
解答
正答は4番
ア 公式① $V=E\ d$ より式変形すれば $E=\cfrac{V}{d}$ となります。これを問題に当てはめれば、
$E_1=\cfrac{V_0}{d}$ と $E_2=\cfrac{V_0}{d}$ となります。
$\varepsilon$ とは無関係です。
イ 公式② $D=\varepsilon\ E$ に $E=\cfrac{V}{d}$ を代入すると $D=\varepsilon\ \cfrac{V}{d}$ となります。
式の見方を変えて $D=\cfrac{\varepsilon}{d}V_0$ ここに $\varepsilon=\varepsilon_r\varepsilon_0$ を代入して
$D=\cfrac{\varepsilon_r\varepsilon_0}{d}V_0$ よって
$D_1=\cfrac{\varepsilon_0\varepsilon_{r1}}{d}V_0$ と $D_2=\cfrac{\varepsilon_0\varepsilon_{r2}}{d}V_0$ となります。
ウ 公式④ $Q=C\ V$ の $C$ に公式③ $C=\varepsilon\:\cfrac{S}{d}$ を代入すると、
$Q=\varepsilon\:\cfrac{S}{d}\ V$ 式の見方を変えて $Q=\cfrac{\varepsilon}{d}\ SV$ となります。
ここに $\varepsilon=\varepsilon_r\varepsilon_0$ を代入すると
$Q=\cfrac{\varepsilon_0\varepsilon_{r}}{d}SV_0$ よって
$Q_1=\cfrac{\varepsilon_0\varepsilon_{r1}}{d}SV_0$ と $Q_2=\cfrac{\varepsilon_0\varepsilon_{r2}}{d}SV_0$ になります。
解説
静電気(コンデンサ)の問題です。
この問題で少し注意するところがあります。それは、比誘電率 $\varepsilon_r$ のところです。
比誘電率 $\varepsilon_r$ はあくまで比であり、単位もありません。よって、比誘電率 $\varepsilon_r$ が単独で出てくることはありません。必ず $\varepsilon_r\varepsilon_0$ の形で出てきます。少し、頭の片隅に置いておいてください。
それでは、公式① $V=E\ d$ 〔V〕から説明していきたいと思います。
ここに出てくる電界の強さEは、別名を電位の傾きと言います。下図のようなイメージです。
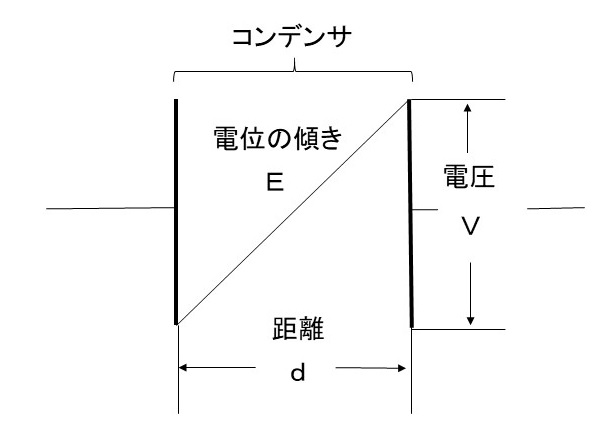
$y=ax$ の $a$ が傾きを表すのと同様に、$V=Ed$ の $E$ が傾きを表します。
次に公式② $D=\varepsilon\ E$ についてです。
「電界の強さ $E$ は」の前に、電界とは「電気力線が走っている場」です。
電界の強さとは、電気力線密度のことです。
では、電気力線とは、架空の線で、Q〔C〕の電荷から $\cfrac{Q}{\varepsilon}$ (本)出てくると規定されています。
一方、電束とは。こちらも架空の線で、誘電率に影響されない、場によって本数が変わらない線です。
よって、Q〔C〕の電荷から $Q$ (本)の電束が出ると規定されています。
このことから、電束密度Dは、$\varepsilon$ 倍の電気力線密度E( $D=\varepsilon E$ )ということになります。
では、公式③ $C=\varepsilon\:\cfrac{S}{d}$ の説明に進みます。
誘電率 $\varepsilon$ は、電荷の溜めやすさの指標でもあります。誘電率 $\varepsilon$ が大きくなると静電容量の大きくなる(比例の)関係にあります。
また、面積Sが大きくなると、溜める面積が増えるので溜まる電荷も増えます。。
その代わりに距離(間隔)dに反比例します。
この面積Sに比例すれば、距離dに反比例する関係はチョクチョク出てきます。
最後の公式④ $Q=C\ V$ についてですが、静電容量Cは容量とあるので静電容量が大きくなると溜まる電荷も増えます。
電圧Vは、電荷を押し込める役割をする(イメージ)ので、電圧が増えれば溜まる電荷も増えます。
以上で、公式の説明を終わります。
テクニック
解説の最初で少し述べましたが、比誘電率 $\varepsilon_r$ が単独で出てくることは、まずありません。
よって、解答の1番及び2番は排除できます。
また、比誘電率 $\varepsilon_r$ が設定されているときに、真空中の誘電率 $\varepsilon_0$ が単独で出てくることもありません。
誘電体が空気のときは、誘電率が真空中の誘電率 $\varepsilon_0$ とほぼ等しく、真空中の誘電率 $\varepsilon_0$ が用いられることが多いので、この式 $Q=\cfrac{\varepsilon_0}{d}SV$ を見慣れている人も多いと思います。
(誘電体が空気なら、この式 $Q=\cfrac{\varepsilon_0}{d}SV$ は正しいです。)
よって、5番も排除できます。
また、公式①だけを覚えていたとしたら、3番4番の二つに絞り込むことができます。
これ以上絞り込むことができなければ(正答を見つけられなければ)、サイコロを振りましょう。
まとめ
この問題の(ア)は公式①そのままで答えが出てきますが、(イ)は公式②に公式①を代入しないと答えが出てきません。
(ウ)に至っては公式④を思いついて、さらに公式③も思いつかないと答えにたどり着けません。
少し面倒くさい部類に入る問題だとおもいます。
まずは、公式を覚えましょう。上の解説が、そのための一助になれば幸いです。
オマケ
公式① $V=E\ d$ の語呂合わせ
ヴィクトリー(V)はエー(E)デー(d)
又は「サインはV」はエー(E)デー(d)(古いですが)
公式② $D=\varepsilon\ E$ の語呂合わせ
ダンディー(D)なエプロン($\varepsilon$ )はイイ(E)
公式③ $C=\varepsilon\:\cfrac{S}{d}$ の語呂合わせ
シークラス(C)のエプロン($\varepsilon$ )MEN(面積S)はパー(/)で(d)した
公式④ $Q=C\ V$ の語呂合わせ
Qちゃん、シ(C)ブ(V)い これに限ります。
ちょっとした遊びを提案します。
1日1つの公式の語呂合わせを考えませんか?
朝1値の公式をメモします。その日1日の隙間時間(例えば寝てはいけない会議の時間、又は電車の待ち時間)を利用して、最低3個の語呂合わせを考えると義務付けます。夜、ノートの1ページに公式と語呂合わせを書いて残しておきましょう。
一巡したら、最初に戻りましょう。

コメント